题目内容
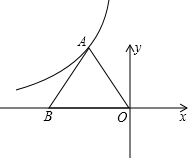
 等边△OAB在直角坐标系中的位置如图所示,折叠三角形使点B与y轴上的点C重合,折痕为MN,且CN平行于x轴,则∠CMN=________度.
等边△OAB在直角坐标系中的位置如图所示,折叠三角形使点B与y轴上的点C重合,折痕为MN,且CN平行于x轴,则∠CMN=________度.
45
分析:易得∠CNO为30°,那么根据折叠可得∠CNM=∠BNM=75°,由∠MCN=∠B=60°,根据三角形内角和可得∠CMN的度数.
解答:∵CN∥x轴,
∴∠OCN=90°,
∵∠BOC=60°,
∴∠CNO=30°,
∴∠CNM+∠BNM=150°,
∴∠CNM=∠BNM=75°,
∵∠MCN=∠B=60°,
∴∠CMN=45度.
故答案为45.
点评:考查折叠问题;用到的知识点为:折叠前后的角相等;注意综合利用平行线性质及三角形内角和定理.
分析:易得∠CNO为30°,那么根据折叠可得∠CNM=∠BNM=75°,由∠MCN=∠B=60°,根据三角形内角和可得∠CMN的度数.
解答:∵CN∥x轴,
∴∠OCN=90°,
∵∠BOC=60°,
∴∠CNO=30°,
∴∠CNM+∠BNM=150°,
∴∠CNM=∠BNM=75°,
∵∠MCN=∠B=60°,
∴∠CMN=45度.
故答案为45.
点评:考查折叠问题;用到的知识点为:折叠前后的角相等;注意综合利用平行线性质及三角形内角和定理.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
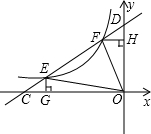
 12、等边△OAB在直角坐标系中的位置如图所示,折叠三角形使点B与y轴上的点C重合,折痕为MN,且CN平行于x轴,则∠CMN=
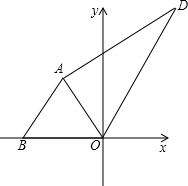
12、等边△OAB在直角坐标系中的位置如图所示,折叠三角形使点B与y轴上的点C重合,折痕为MN,且CN平行于x轴,则∠CMN= 如图,等边△ABC在直角坐标系xOy中,已知A(2,0),B(-2,0),点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是
如图,等边△ABC在直角坐标系xOy中,已知A(2,0),B(-2,0),点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是