Question

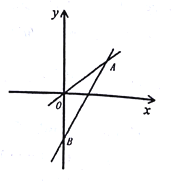
【题目】如图，一次函数的图象与轴交于点，与正比例函数的图象相交于点，且.

（1）分别求出这两个函数的解析式；

（2）求的面积；

（3）点在轴上，且是等腰三角形，请直接写出点的坐标.

Answer 1

【答案】（1）；；（2）10；（3）或或或

【解析】

（1）根据点A坐标，可以求出正比例函数解析式，再求出点B坐标即可求出一次函数解析式．

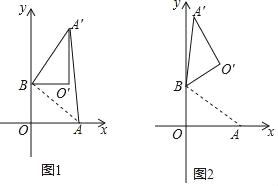
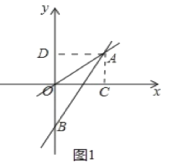
（2）如图1中，过A作AD⊥y轴于D，求出AD即可解决问题．

（3）分三种情形讨论即可①OA=OP，②AO=AP，③PA=PO．

解：（1）正比例函数的图象经过点，

，

，

正比例函数解析式为

如图1中，过作轴于，

在中，，

解得

一次函数解析式为

（2）如图1中，过作轴于，

（3）)如图2中,当OP=OA时,P(5,0),P (5,0)，

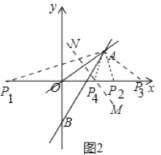
当AO=AP时,P (8,0),

当PA=PO时,线段OA的垂直平分线为y= ，

∴P，

∴满足条件的点P的坐标或或或