题目内容
25、已知:如图①,现有a×a,b×b的正方形纸片和a×b的长方形纸片各若干块.

(1)图②是用这些纸片拼成的一个长方形,(每两个纸片之间既不重叠,也无空隙),利用这个长方形的面积,写出一个代数恒等式
(2)试选用图①中的纸片(每种纸片至少用一次)在下面的方框中拼成与图②不同的一个长方形,(拼出的图中必须保留拼图的痕迹),标出此长方形的长和宽,并利用拼成的长方形面积写出一个代数恒等式.


(1)图②是用这些纸片拼成的一个长方形,(每两个纸片之间既不重叠,也无空隙),利用这个长方形的面积,写出一个代数恒等式
(a+b)(a+2b)=a2+3ab+2b2
;(2)试选用图①中的纸片(每种纸片至少用一次)在下面的方框中拼成与图②不同的一个长方形,(拼出的图中必须保留拼图的痕迹),标出此长方形的长和宽,并利用拼成的长方形面积写出一个代数恒等式.

分析:(1)由图中大矩形的面积=中间的各图片的面积的和,就可得出代数式.
(2)拼法较多,可根据小图片的面积和要拼成的大矩形的面积进行比较可得出需要的小图片的张数,然后进行拼接,得出代数式.
(2)拼法较多,可根据小图片的面积和要拼成的大矩形的面积进行比较可得出需要的小图片的张数,然后进行拼接,得出代数式.
解答:解:
(1)代数恒等式:(a+b)(a+2b)=a2+3ab+2b2;
(2)答案不唯一:

(a+3b)(a+b)=a2+4ab+3b2(2a+b)(a+b)=2a2+3ab+b2.

(1)代数恒等式:(a+b)(a+2b)=a2+3ab+2b2;
(2)答案不唯一:

(a+3b)(a+b)=a2+4ab+3b2(2a+b)(a+b)=2a2+3ab+b2.
点评:此题考查的内容是整式的运算与几何的综合题.此题的立意较新颖,注意对此类问题的深入理解.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
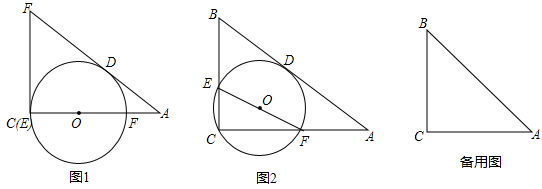
 27、已知:如图,在⊙O中,OA是半径,CD是弦,OA交CD于点E.现有四个条件:①∠COA=∠AOD=60°;②AC=AD=OA;③点E分别是AO、CD的中点;④OA⊥CD.
27、已知:如图,在⊙O中,OA是半径,CD是弦,OA交CD于点E.现有四个条件:①∠COA=∠AOD=60°;②AC=AD=OA;③点E分别是AO、CD的中点;④OA⊥CD.
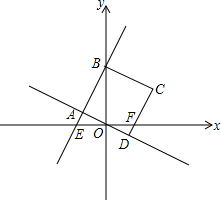 已知:如图,直线y=2x+b与x轴、y轴分别相交于点E、点B(0,3).
已知:如图,直线y=2x+b与x轴、y轴分别相交于点E、点B(0,3). 已知,如图,A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,你知道C点对应的数是m;若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的D点相遇,你知道D点对应的数是n,则m+n=
已知,如图,A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,你知道C点对应的数是m;若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的D点相遇,你知道D点对应的数是n,则m+n=