题目内容
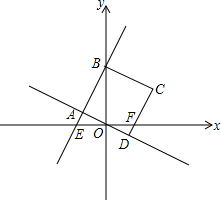 已知:如图,直线y=2x+b与x轴、y轴分别相交于点E、点B(0,3).
已知:如图,直线y=2x+b与x轴、y轴分别相交于点E、点B(0,3).(1)填空:b=
3
3
;(2)若直线y=-
| 1 |
| 2 |
①求∠OAB的度数;
②在直线AB的右侧作菱形ABCD,现有抛物线y=(x-m)2+n的顶点T在直线y=-
| 1 |
| 2 |
分析:(1)由于直线y=2x+b的函数图象经过点B,将点B的坐标代入直线的解析式中,即可确定b的值.
(2)①首先联立这两条直线的解析式得到点A的坐标;进一步能求出线段OA、AB的长,OB的长易知,然后根据这三边的长判断∠OAB的度数;
②由①知,AB=AD=2OA,那么点O是线段AD的中点,此时发现点A、D关于点O对称,则点D的坐标可得;通过观察图示不难看出,当点T、A重合时,抛物线与线段AB、AD都相交(交于一个公共点A),即m的最小值与点A的横坐标相同,因此只需判断m的最大值即可;此时需要分两步考虑:
Ⅰ、当抛物线的对称轴左侧图象经过点B时,先求出m的值,即可确定抛物线的解析式,然后再判断抛物线的图象是否与线段AD相交,若相交,那么此时的m值即为最大值,若不想交,再考虑下一步;
Ⅱ、当抛物线的对称轴左侧图象经过点D时,方法同上.
(2)①首先联立这两条直线的解析式得到点A的坐标;进一步能求出线段OA、AB的长,OB的长易知,然后根据这三边的长判断∠OAB的度数;
②由①知,AB=AD=2OA,那么点O是线段AD的中点,此时发现点A、D关于点O对称,则点D的坐标可得;通过观察图示不难看出,当点T、A重合时,抛物线与线段AB、AD都相交(交于一个公共点A),即m的最小值与点A的横坐标相同,因此只需判断m的最大值即可;此时需要分两步考虑:
Ⅰ、当抛物线的对称轴左侧图象经过点B时,先求出m的值,即可确定抛物线的解析式,然后再判断抛物线的图象是否与线段AD相交,若相交,那么此时的m值即为最大值,若不想交,再考虑下一步;
Ⅱ、当抛物线的对称轴左侧图象经过点D时,方法同上.
解答:解:(1)由题意知,直线y=2x+b经过点B(0,3),则有:
2×0+b=3,b=3;
故填:3.
(2)①联立y=-
x与y=2x+3,得:
,
解得
则点A(-
,
);
则:OA2=(-
)2+(
)2=
,AB2=(-
)2+(3-
)2=
,OB2=32=9;
则OA2+AB2=OB2,即∠OAB=90°.
②依题意,点T(m,n)在直线y=-
x上,那么 n=-
m,即抛物线的解析式:y=(x-m)2-
m,点T(m,-
m);
在Rt△OBE中,OE=
,OB=3,∴tan∠OBE=
,AB=2OA;
由于四边形ABCD是菱形,那么AD=AB=2OA,即点O是线段AD的中点,则点D(
,-
).
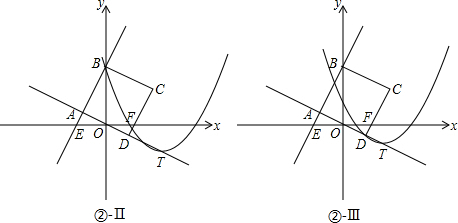 Ⅰ、当点T、A重合时,抛物线同时经过线段AB、AD,此时m=-
Ⅰ、当点T、A重合时,抛物线同时经过线段AB、AD,此时m=-
;
Ⅱ、当抛物线的对称轴左侧图象经过点B时,有:
(0-m)2-
m=3,解得:m1=2、m2=-
(舍);
故抛物线:y=(x-2)2-1;
当x=
时,y=(
-2)2-1=-
>-
,
所以抛物线只与线段AB相交,不与线段AD相交,不合题意;
Ⅲ、当抛物线的对称轴左侧图象经过点D时,由Ⅱ知,抛物线的图象与线段AB、AD都相交;
将点(
,-
)代入y=(x-m)2-
m中,有:
(
-m)2-
m=-
,解得:m1=
,m2=
(舍);
综上,m的取值范围:-
≤m≤
.
2×0+b=3,b=3;
故填:3.
(2)①联立y=-
| 1 |
| 2 |
|
解得
|
则点A(-
| 6 |
| 5 |
| 3 |
| 5 |
则:OA2=(-
| 6 |
| 5 |
| 3 |
| 5 |
| 9 |
| 5 |
| 6 |
| 5 |
| 3 |
| 5 |
| 36 |
| 5 |
则OA2+AB2=OB2,即∠OAB=90°.
②依题意,点T(m,n)在直线y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OBE中,OE=
| 3 |
| 2 |
| 1 |
| 2 |
由于四边形ABCD是菱形,那么AD=AB=2OA,即点O是线段AD的中点,则点D(
| 6 |
| 5 |
| 3 |
| 5 |
 Ⅰ、当点T、A重合时,抛物线同时经过线段AB、AD,此时m=-
Ⅰ、当点T、A重合时,抛物线同时经过线段AB、AD,此时m=-| 6 |
| 5 |
Ⅱ、当抛物线的对称轴左侧图象经过点B时,有:
(0-m)2-
| 1 |
| 2 |
| 3 |
| 2 |
故抛物线:y=(x-2)2-1;
当x=
| 6 |
| 5 |
| 6 |
| 5 |
| 9 |
| 25 |
| 3 |
| 5 |
所以抛物线只与线段AB相交,不与线段AD相交,不合题意;
Ⅲ、当抛物线的对称轴左侧图象经过点D时,由Ⅱ知,抛物线的图象与线段AB、AD都相交;
将点(
| 6 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
(
| 6 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| 17 |
| 10 |
| 6 |
| 5 |
综上,m的取值范围:-
| 6 |
| 5 |
| 17 |
| 10 |
点评:此题的难点在于最后一题,解题的关键是判断m取最大、最小值时,抛物线的图象经过了哪些点;在求m的最大取值时,容易出现错误,有些同学很可能将点D的横坐标直接视为m的最大值,但忽视了抛物线对称轴左侧图象经过点D时的情况,这就需要通过图示作出正确的判断.

练习册系列答案
相关题目
 原点O及A、B两点.
原点O及A、B两点. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线y=kx+b经过点A、B.
已知:如图,直线y=kx+b经过点A、B. 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线 已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x-5)°,那么∠1=
已知:如图,直线a∥b,∠1=(2x+10)°,∠2=(3x-5)°,那么∠1=