题目内容
如图(1),分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为 轴、
轴、 轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在
轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在 轴上)交y轴于另一点Q,抛物线
轴上)交y轴于另一点Q,抛物线 经过A、C两点,与
经过A、C两点,与 轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
轴的另一交点为G,M是FG的中点,B点坐标为(2,2).【小题1】求抛物线的函数解析式和点E的坐标;
【小题2】求证:ME是⊙P的切线;

【小题1】解:如图甲,连接PE、PB,设PC=n,

∵正方形CDEF的面积为1,
∴CD=CF=1,
根据圆和正方形的对称性知:OP=PC=n,
∴BC=2PC=2n,
∵而PB=PE,
∴PB2=BC2+PC2=4n2+n2=5n2,PE2=PF2+EF2=(n+1)2+1,
∴5n2=(n+1)2+1,
解得:n=1或n=-
 (舍去),
(舍去),∴BC=OC=2,
∴B点坐标为(2,2);(6分)
【小题2】证明:如图甲,由(1)知A(0,2),C(2,0),
∵A,C在抛物线上,
∴
 ,
,解得:
 ,
,∴抛物线的解析式为:y=
 x2-
x2- x+2=
x+2= (x-3)2-
(x-3)2- ,
,∴抛物线的对称轴为x=3,即EF所在直线,
∵C与G关于直线x=3对称,
∴CF=FG=1,
∴MF=
 FG=
FG= ,
,在Rt△PEF与Rt△EMF中,
∠EFM=∠EFP,
∵
 ,
, ,
,∴
 ,
,∴△PEF∽△EMF,
∴∠EPF=∠FEM,
∴∠PEM=∠PEF+∠FEM=∠PEF+∠EPF=90°,
∴ME是⊙P的切线;(12分)解析:
(1)如图甲,连接PE、PB,设PC=n,由正方形CDEF的面积为1,可得CD=CF=1,根据圆和正方形的对称性知:OP=PC=n,由PB=PE,根据勾股定理即可求得n的值,继而求得B的坐标;
(2)由(1)知A(0,2),C(2,0),即可求得抛物线的解析式,然后求得FM的长,则可得△PEF∽△EMF,则可证得∠PEM=90°,即ME是⊙P的切线;

练习册系列答案
相关题目
 (2012•新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积
(2012•新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积 如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=
如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=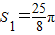 ,S2=2π,则S3是 .
,S2=2π,则S3是 .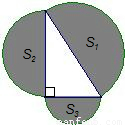
 ,S2=2π,则S3是 .
,S2=2π,则S3是 .
 ,S2=2π,则S3是 .
,S2=2π,则S3是 .