题目内容
等边三角形的内切圆与它的外接圆的半径比是( )
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、2 |
考点:三角形的内切圆与内心,三角形的外接圆与外心
专题:
分析:首先根据题意画出图形,再作出辅助线OD、OE,证明△AOD为直角三角形且∠OAD为30°,即可求出OD、OA的比.
解答: 解:如图,连接OD、OE;
解:如图,连接OD、OE;
∵AB、AC切圆O与E、D,
∴OE⊥AB,OD⊥AC,
∵AO=AO,EO=DO,
∴△AEO≌△ADO(HL),
∴∠DAO=∠EAO;
又∵△ABC为等边三角形,
∴∠BAC=60°,
∴∠OAC=
×60°=30°,
∴OD:AO=1:2.
∴等边三角形的内切圆与外接圆半径的比是
,
故选B.
 解:如图,连接OD、OE;
解:如图,连接OD、OE;∵AB、AC切圆O与E、D,
∴OE⊥AB,OD⊥AC,
∵AO=AO,EO=DO,
∴△AEO≌△ADO(HL),
∴∠DAO=∠EAO;
又∵△ABC为等边三角形,
∴∠BAC=60°,
∴∠OAC=
| 1 |
| 2 |
∴OD:AO=1:2.
∴等边三角形的内切圆与外接圆半径的比是
| 1 |
| 2 |
故选B.
点评:本题考查了三角形的内切圆与外接圆的知识,解答此题要找到直角三角形,将三角形内切圆和三角形外接圆联系起来是解题的关键,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
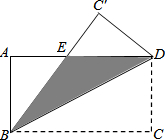 如图,在矩形ABCD中,AB=3,AD=5,现将该矩形沿对角线BD折叠,使得点C落在点C′处,BC′边交AD边于点E,请求出图中阴影部分的面积.
如图,在矩形ABCD中,AB=3,AD=5,现将该矩形沿对角线BD折叠,使得点C落在点C′处,BC′边交AD边于点E,请求出图中阴影部分的面积.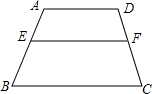 如图,在梯形ABCD中,AD∥BC,EF∥BC,若AD=12cm,BC=17cm,AE:EB=2:3,则EF=
如图,在梯形ABCD中,AD∥BC,EF∥BC,若AD=12cm,BC=17cm,AE:EB=2:3,则EF= 如图所示,已知AB∥A′B′,BC∥B′C′,求证:△OAC∽△OA′C′.
如图所示,已知AB∥A′B′,BC∥B′C′,求证:△OAC∽△OA′C′.