题目内容
 如图,C是⊙O的直径AB延长线上一点,CD是⊙O的切线,D是切点.已知AB=2,∠BAD=30°,那么BC=
如图,C是⊙O的直径AB延长线上一点,CD是⊙O的切线,D是切点.已知AB=2,∠BAD=30°,那么BC=
- A.2
- B.

- C.1
- D.

C
分析:连接OD,得出∠ODC=90°,根据OA=OD求出∠A=∠ODA=30°,求出∠BOD=60°,根据三角形的内角和定理求出∠C,根据含30度角的直角三角形性质求出OC,即可求出BC.
解答: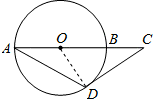 解:
解:
连接OD,
∵AB=2,
∴OA=OB=OD=1,
∵OA=OD,
∴∠BAD=∠ODA=30°,
∴∠DOB=∠BAD+∠ODA=60°,
∵CD切⊙O于D,
∴∠ODC=90°,
∴∠C=180°-90°-60°=30°,
∴OC=2OD=2,
∴BC=2-1=1,
故选C.
点评:本题考查了含30度角的直角三角形、三角形的外角性质、三角形的内角和定理、切线的性质等知识点,关键是求出∠C=30°,题目具有一定的代表性,是一道综合性比强的题目.
分析:连接OD,得出∠ODC=90°,根据OA=OD求出∠A=∠ODA=30°,求出∠BOD=60°,根据三角形的内角和定理求出∠C,根据含30度角的直角三角形性质求出OC,即可求出BC.
解答:
 解:
解:连接OD,
∵AB=2,
∴OA=OB=OD=1,
∵OA=OD,
∴∠BAD=∠ODA=30°,
∴∠DOB=∠BAD+∠ODA=60°,
∵CD切⊙O于D,
∴∠ODC=90°,
∴∠C=180°-90°-60°=30°,
∴OC=2OD=2,
∴BC=2-1=1,
故选C.
点评:本题考查了含30度角的直角三角形、三角形的外角性质、三角形的内角和定理、切线的性质等知识点,关键是求出∠C=30°,题目具有一定的代表性,是一道综合性比强的题目.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=35°,则∠D=
如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=35°,则∠D= 如图,AC是⊙O的直径,BD是⊙O的弦,EC∥AB,交⊙O于E.图中与∠BOC的一半相等的角有
如图,AC是⊙O的直径,BD是⊙O的弦,EC∥AB,交⊙O于E.图中与∠BOC的一半相等的角有 如图,AB是⊙O的直径,D为弧AC的中点,∠B=50°,则∠DAC=
如图,AB是⊙O的直径,D为弧AC的中点,∠B=50°,则∠DAC= 如图,AB是⊙O的直径,∠ABC=30°,OA=2,则BC长为
如图,AB是⊙O的直径,∠ABC=30°,OA=2,则BC长为 如图:P是⊙O的直径BA延长线上一点,PD交⊙O于点C,且PC=OD,如果∠P=24°,则∠DOB=
如图:P是⊙O的直径BA延长线上一点,PD交⊙O于点C,且PC=OD,如果∠P=24°,则∠DOB=