题目内容
已知(a-| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:①由于(a-
)2≥0且|a+b+3|≥0,所以(a-
)2+|a+b+3|=0可得a-
=0,a+b+3=0解这两个方程求出a,b的值;
②观察代数式比较复杂,应先化简,再将a,b的值代入化简后的代数式求出原代数式的值.
| 1 |
| a |
| 1 |
| a |
| 1 |
| 2 |
②观察代数式比较复杂,应先化简,再将a,b的值代入化简后的代数式求出原代数式的值.
解答:解:因为(a-
)2+|a+b+3|=0,
所以
解得a=
,b=-
;
原式=(-a2+3ab-
b2)-(-2a2+4ab-
b2)
=-a2+3ab-
b2+2a2-4ab+
b2
=a2-ab,
当a=
,b=-
时,
原式=(
)2-
×(-
)=
+
=2.
| 1 |
| 2 |
所以
|
| 1 |
| 2 |
| 7 |
| 2 |
原式=(-a2+3ab-
| 1 |
| 2 |
| 1 |
| 2 |
=-a2+3ab-
| 1 |
| 2 |
| 1 |
| 2 |
=a2-ab,
当a=
| 1 |
| 2 |
| 7 |
| 2 |
原式=(
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 4 |
| 7 |
| 4 |
点评:本题主要考查平方式和绝对值的意义及通过化简,代入法求解代数式的值.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
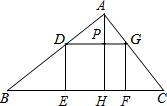 如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.
如图,矩形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8.当矩形DEFG面积最大时,求矩形的长和宽.