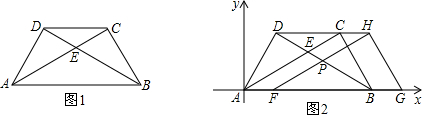
题目内容
 四边形ABCD是正方形,△ABF旋转后与△CBE重合.
四边形ABCD是正方形,△ABF旋转后与△CBE重合.
(1)旋转中心是______,旋转角等于______;
(2)若AF=1,BC=3,求EF的长.
解:(1)由图可知,旋转中心是B,对应边AB、BC的夹角为旋转角,
在正方形ABCD中,∠ABC=90°,
所以旋转角等于90°.
故答案为:B;90°.
(2)在正方形ABCD中,AB=BC=3,
在Rt△ABF中,BF= =
= =
= ,
,
∵△ABF旋转后与△CBE重合,
∴BE=BF,∠EBF=∠ABC=90°,
∴△BEF是等腰直角三角形,
在Rt△BEF中,EF= =
= =2
=2 .
.
分析:(1)根据图形可以确定点B为旋转中心,对应边AB、BC的夹角为旋转角;
(2)根据正方形的四条边都相等可得AB=BC,利用勾股定理求出BF,再判断出△BEF是等腰直角三角形,然后利用勾股定理列式进行计算即可得解.
点评:本题考查了旋转的性质,正方形的性质,勾股定理的应用,是基础题,(2)确定出△BEF是等腰直角三角形是解题的关键.
在正方形ABCD中,∠ABC=90°,
所以旋转角等于90°.
故答案为:B;90°.
(2)在正方形ABCD中,AB=BC=3,
在Rt△ABF中,BF=
 =
= =
= ,
,∵△ABF旋转后与△CBE重合,
∴BE=BF,∠EBF=∠ABC=90°,
∴△BEF是等腰直角三角形,
在Rt△BEF中,EF=
 =
= =2
=2 .
.分析:(1)根据图形可以确定点B为旋转中心,对应边AB、BC的夹角为旋转角;
(2)根据正方形的四条边都相等可得AB=BC,利用勾股定理求出BF,再判断出△BEF是等腰直角三角形,然后利用勾股定理列式进行计算即可得解.
点评:本题考查了旋转的性质,正方形的性质,勾股定理的应用,是基础题,(2)确定出△BEF是等腰直角三角形是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目