题目内容
 如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO等于
如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO等于
- A.70°
- B.64°
- C.62°
- D.51°
B
分析:连接OC.证明∠CAO=∠OAB=∠BAD,从而进一步求解.
解答: 解:连接OC.
解:连接OC.
则OC=OB,AC=AB,OA=OA,△AOC≌△AOB.
∴∠CAO=∠BAO.
∵AB是⊙O的切线,
∴OB⊥AB.
∵BD=OB,
∴AB是线段OD的垂直平分线,OA=AD.
∴∠OAB=∠DAB=∠OAC= ×78°=26°.
×78°=26°.
∠ADO=180°-∠ABD-∠DAB=180°-90°-26°=64°.
故选B.
点评:本题考查了圆的切线性质,及等腰三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
分析:连接OC.证明∠CAO=∠OAB=∠BAD,从而进一步求解.
解答:
 解:连接OC.
解:连接OC.则OC=OB,AC=AB,OA=OA,△AOC≌△AOB.
∴∠CAO=∠BAO.
∵AB是⊙O的切线,
∴OB⊥AB.
∵BD=OB,
∴AB是线段OD的垂直平分线,OA=AD.
∴∠OAB=∠DAB=∠OAC=
 ×78°=26°.
×78°=26°.∠ADO=180°-∠ABD-∠DAB=180°-90°-26°=64°.
故选B.
点评:本题考查了圆的切线性质,及等腰三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
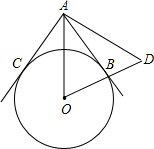 如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO等于( )
如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO等于( )| A、70° | B、64° | C、62° | D、51° |
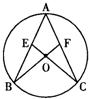
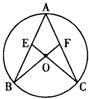 16、如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.
16、如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.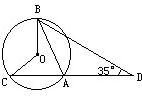 30、如图,AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,则∠BOC=
30、如图,AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,则∠BOC= 如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.求证:CE=BF.
如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.求证:CE=BF.