题目内容
【题目】已知
、
、
、
、
五个点，抛物线
经过其中的三个点．
（1）求证：点
、
不能同时在抛物线上；
（2）点
在抛物线上吗？为什么？
【答案】（1）证明见解析；（2）不在，理由见解析．
【解析】
（1）由抛物线y=a（x-1）2+k可知，抛物线对称轴为x=1，顶点为
，假设点点
同时在抛物线
上，然后将C（-1，2），E（4，2）两点代入解析式中求得a的值，得出矛盾，从而假设不成立，不能同时在抛物线上；
（2）假设A点在抛物线上，根据抛物线的性质得出点A为抛物线最低点，抛物线经过A，C，E三点，从而产生矛盾，排除A点在抛物线上．
解：
（1）
对称轴为
，顶点为
设点同时在抛物线上，
当
时，
当
时，
这与
矛盾
假设不成立，不能同时在抛物线上
（2）不在
理由：若点
在抛物线上
由（1）得，抛物线的顶点坐标为
为顶点
为最低点
又
抛物线过
中的三点
而B（0，-1），C（-1，2），D（2，-1），E（4，2）
抛物线只能过
三点，这与（1）中的结论矛盾
假设不成立，点不在抛物线上．
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案【题目】某数学兴趣小组在探究函数y=|x2-4x+3|的图象和性质时，经历以下几个学习过程：
(1)列表(完成以下表格)
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y1=x2-4x+3 | … | 15 | 8 | 0 | 0 | 3 | 15 | … | |||
y=|x2-4x+3| | … | 15 | 8 | 0 | 0 | 3 | 15 | … |
(2)描点并画出函数图象草图(在备用图1中描点并画图)
(3)根据图象完成以下问题
(ⅰ)观察图象
函数y=|x2-4x+3|的图象可由函数y1=x2-4x+3的图象如何变化得到？
答：______．
(ⅱ)数学小组探究发现直线y=8与函数y=|x2-4x+3|的图象交于点E、F，E(-1，8)，F(5，8)，则不等式|x2-4x+3|＞8的解集是______；
(ⅲ)设函数y=|x2-4x+3|的图象与x轴交于A、B两点(B位于A的右侧)，与y轴交于点C．
①求直线BC的解析式；
②探究应用：将直线BC沿y轴平移m个单位后与函数y=|x2-4x+3|的图象恰好有3个交点，求此时m的值．
【题目】某校为了预测本校九年级男生毕业体育测试达标情况，随机抽取该年级部分男生进行了一次测试（满分50分，成绩均记为整数分），并按测试成绩
（单位：分）分成四类：
类（
），
类（
），
类（
），
类（
）绘制出如图所示的不完整条形统计图，请根据图中信息解答下列问题：
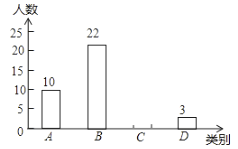
成绩等级 | 人数 | 所占百分比 |
| 10 |
|
| 22 |
|
|
|
|
| 3 |
|
（1）
______，
_______，
_________；
（2）补全条形统计图；
（3）若该校九年级男生有600名，类为测试成绩不达标，请估计该校九年级男生毕业体育测试成绩能达标的有多少名？
