题目内容
设a2-b2=1+| 2 |
| 2 |
分析:把所给代数式整理为和a2-b2,b2-c2,a2-c2有关的形式,把相关数值代入求值即可.
解答:解:∵a2-b2=1+
①;b2-c2=1-
②;
∴①+②得:a2-c2=2,
∴原式=
=
=5,
故答案为5.
| 2 |
| 2 |
∴①+②得:a2-c2=2,
∴原式=
| (a2-b2)2+(b2-c2)2+ (a2-c2)2 |
| 2 |
3+2
| ||||
| 2 |
故答案为5.
点评:考查代数式的求值,把所给代数式整理为和a2-b2,b2-c2,a2-c2有关的形式是解决本题的关键.

练习册系列答案
相关题目
 ,求a2+
,求a2+ -2的值.
-2的值. 的值.
的值. +
+ =
= ,
, =
= -
-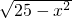 -
- =2,求
=2,求 的值等于 .
的值等于 .