题目内容
 已知长方形ABCD,AB=3cm,AD=4cm,过对角线BD的中点O做BD垂直平分线EF,分别交AD、BC于点E、F,则AE的长为________.
已知长方形ABCD,AB=3cm,AD=4cm,过对角线BD的中点O做BD垂直平分线EF,分别交AD、BC于点E、F,则AE的长为________.
 cm
cm分析:连接EB,构造直角三角形,设AE为x,则DE=BE=4-x,利用勾股定理得到有关x的一元一次方程,求得即可.
解答:
 解:连接EB,
解:连接EB,∵EF垂直平分BD,
∴ED=EB,
设AE=xcm,则DE=EB=(4-x)cm,
在Rt△AEB中,
AE2+AB2=BE2,
即:x2+32=(4-x)2,
解得:x=

故答案为:
 cm.
cm.点评:本题考查了勾股定理的内容,利用勾股定理不单单能在直角三角形中求边长,而且能利用勾股定理这一隐含的等量关系列出方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 等?
等?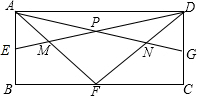 如图,在长方形ABCD中,E、F、G分别是边AB、BC、CD的中点.已知长方形ABCD的面积是40cm2.则四边形MFNP的面积是
如图,在长方形ABCD中,E、F、G分别是边AB、BC、CD的中点.已知长方形ABCD的面积是40cm2.则四边形MFNP的面积是 如图,已知长方形ABCD四个顶点的坐标分别是A(2,-2
如图,已知长方形ABCD四个顶点的坐标分别是A(2,-2 如图所示,已知长方形ABCD,点A′是长方形ABCD平移后点A的对应点,作出平移后的长方形A′B′C′D′.
如图所示,已知长方形ABCD,点A′是长方形ABCD平移后点A的对应点,作出平移后的长方形A′B′C′D′.