题目内容
若等腰三角形的一个内角为50°,则这个三角形顶角的大小为分析:(1)已知中的50°内角有可能为底角,也有可能为顶角,然后根据三角形的内角定理,即可推出结论;
(2)根据三角形的三边关系,推出腰长和底边,由2+2<5,即可推出腰长应为5,底边长为2,即可计算出周长.
(2)根据三角形的三边关系,推出腰长和底边,由2+2<5,即可推出腰长应为5,底边长为2,即可计算出周长.
解答:解:(1)①当顶角=50°时,
底角=
=65°,
②当底角=50°时,
顶角=180°-2×50°=80°;
(2)假设腰长=2,
∵2+2<5,
∴假设错误,
当腰长=5时,
5+5>2,
5-2<5,
∴假设成立,
∴周长=5+5+2=12cm.
故答案为80°或50°;12.
底角=
| 180°-50° |
| 2 |
②当底角=50°时,
顶角=180°-2×50°=80°;
(2)假设腰长=2,
∵2+2<5,
∴假设错误,
当腰长=5时,
5+5>2,
5-2<5,
∴假设成立,
∴周长=5+5+2=12cm.
故答案为80°或50°;12.
点评:本题主要考查三角形内角和定理,三角形三边关系,关键在于讨论推出顶角或底角的度数,根据三角形三边关系推出腰长和底边长.

练习册系列答案
相关题目
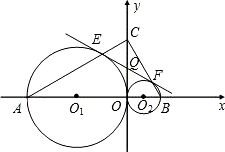 在x轴上是否存在点P,使得△PMN是一个以MN为一直角边的等腰直角三角形?若存在,求出P点坐标;若不存在,请说明理由.
在x轴上是否存在点P,使得△PMN是一个以MN为一直角边的等腰直角三角形?若存在,求出P点坐标;若不存在,请说明理由. (1)如图,已知∠AOB=40°,P为OB上的一点,在∠AOB内,求作一个以OP为底边,底角为20°的等腰三角形OCP(尺规作图,要求保留作图痕迹,不必写出作法).
(1)如图,已知∠AOB=40°,P为OB上的一点,在∠AOB内,求作一个以OP为底边,底角为20°的等腰三角形OCP(尺规作图,要求保留作图痕迹,不必写出作法). 已知一次函数y=2x-1和反比例函数y=
已知一次函数y=2x-1和反比例函数y= 在实数范围内有意义,则x的取值范围是x>1;
在实数范围内有意义,则x的取值范围是x>1;