题目内容
若
+b2+2b+1=0,求a2+
-|b|
| a2-3a+1 |
| 1 |
| a2 |
考点:配方法的应用,非负数的性质:偶次方,非负数的性质:算术平方根
专题:
分析:先利用配方法得到
+(b+1)2=0,则根据几个非负数和的性质得a2-3a+1=0,b+1=0,变形或解方程得a+
=3,b=-1,然后再利用配方法得到原式|=(a+
)2-2-|b|,再利用整体代入的方法计算.
| a2-3a+1 |
| 1 |
| a |
| 1 |
| a |
解答:解:∵
+b2+2b+1=0,
∴
+(b+1)2=0,
∴a2-3a+1=0,b+1=0,
∴a+
=3,b=-1,
∴a2+
-|b|=(a+
)2-2-|b|
=32-2-|-1|
=6.
| a2-3a+1 |
∴
| a2-3a+1 |
∴a2-3a+1=0,b+1=0,
∴a+
| 1 |
| a |
∴a2+
| 1 |
| a2 |
| 1 |
| a |
=32-2-|-1|
=6.
点评:本题考查了配方法的应用:用配方法解一元二次方程或把代数式配成非负数的形式等;配方法的理论依据是公式a2±2ab+b2=(a±b)2.也考查了几个非负数和的性质.

练习册系列答案
相关题目
 已知:点D在AB上,点E在AC上,AB=AC,BE⊥AC,CD⊥AB,求证:BD=CE.
已知:点D在AB上,点E在AC上,AB=AC,BE⊥AC,CD⊥AB,求证:BD=CE. 已知:点D,E,F分别是△ABC中AB,BC,CA边的中点,四边形DECF是菱形,求证:△ABC是等腰三角形.
已知:点D,E,F分别是△ABC中AB,BC,CA边的中点,四边形DECF是菱形,求证:△ABC是等腰三角形. 如图,在Rt△ABC中,∠ACB=90°,DE、DF是△ABC的中位线,连接EF、CD.求证:EF=CD.
如图,在Rt△ABC中,∠ACB=90°,DE、DF是△ABC的中位线,连接EF、CD.求证:EF=CD.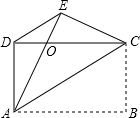 如图,四边形ABCD中,AD=BC,AB=DC,把四边形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
如图,四边形ABCD中,AD=BC,AB=DC,把四边形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.