题目内容
定义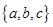
为函数
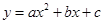的“特征数”．如：函数
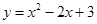的“特征数”是
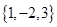，函数
的“特征数”是
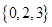,函数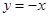
的“特征数”是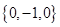
（1）将“特征数”是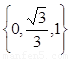
的函数图象向下平移2个单位，得到一个新函数，这个新
函数的解析式是 ；
（2）在（1）中，平移前后的两个函数分别与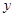
轴交于A、B两点，与直线
分别交于
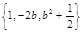D、C两点，在给出的平面直角坐标系中画出图形，判断以A、B、C、D四点为顶点的四边形形状，并说明理由；
（3）若（2）中的四边形与“特征数”是的函数图象有交点，试求出实数
b 的取值范围.
【答案】
（1）
（2）菱形
理由（略） （3）
【解析】（1）根据函数“特征数”写出函数的解析式，再根据平移后一次函数的变化情况写出函数图象向下平移2个单位的新函数的解析式．
（2）判断以A、B、C、D四点为顶点的四边形形状，可根据一次函数图象向下平移2个单位与原函数图象的关系，得出AB=2，并确定为平行四边形，由直线相交计算交点坐标后，求出线段BC=2，再根据菱形的判定（邻边相等的平行四边形是菱形）得出；
（3）根据函数“特征数”写出二次函数的解析式，化为顶点式为y=（x-b）2+ 
，确定二次函数的图象不会经过点B和点C，再将菱形顶点A（0，1），D（
，2）代入二次函数解析式得出实数b的取值范围．
练习册系列答案
相关题目
，
，
] 的函数的一些结论：①当
时，函数图象的顶点坐标是
；②当
时，函数在
时，
随
的增大而减小；③无论m取何值，函数图象都经过同一个点. 其中所有的正确结论有 .（填写正确结论的序号） 
]为函数
的特征数，下面给出特征数为[
，
，
] 的函数的一些结论：①当
时，函数图象的顶点坐标是
；②当
时，函数在
时，
随
的增大而减小；③无论m取何值，函数图象都经过同一个点. 其中所有的正确结论有 .（填写正确结论的序号） 
]为函数
的特征数，下面给出特征数为[
，
，
] 的函数的一些结论：①当
时，函数图象的顶点坐标是
；②当
时，函数在
时，
随
的增大而减小；③无论m取何值，函数图象都经过同一个点. 其中所有的正确结论有 .（填写正确结论的序号） 
]为函数
的特征数，下面给出特征数为[
，
，
] 的函数的一些结论：①当
时，函数图象的顶点坐标是
；②当
时，函数在
时，
随
的增大而减小；③无论m取何值，函数图象都经过同一个点. 其中所有的正确结论有
.（填写正确结论的序号）