题目内容
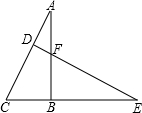 如图,Rt△ABC中,sinA=
如图,Rt△ABC中,sinA= ,AB=12,延长CB至E,作ED⊥AC交AB于F.若BC=BF,则下列结论不成立的是
,AB=12,延长CB至E,作ED⊥AC交AB于F.若BC=BF,则下列结论不成立的是
- A.△ABC≌△EBF
- B.
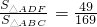
- C.
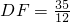
- D.△ADF与△EBF的相似比为
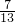
C
分析:根据全等三角形的判定和性质、相似三角形的判定和性质以及锐角三角函数逐项分析即可.
解答:∵ED⊥AC,
∴∠ADF=90°,
∴∠A+∠BFE=90°,
∵∠ABE=90°,
∴∠E+∠BFE=90°,
∴∠A=∠E,
∵在△ABC和△EBF中,
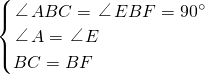 ,
,
∴△ABC≌△EBF(AAS),故A正确;
∵sinA= ,AB=12,
,AB=12,
∴BC=5,AC=13,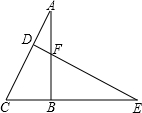
∵∠A=∠A,∠ASDF=∠ABC=90°,
∴△ADF∽ABC,
∴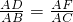 ,
,
∵BC=BF,
∴BF=5,
∴AF=12-5=7,
∴ =
=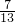 ,
,
∴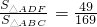 ,故B正确;
,故B正确;
∵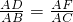 =
=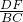 =
=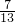 ,
,
∴DF=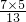 =
=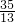 ,故C错误;
,故C错误;
∵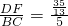 =
=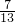 ,
,
∴△ADF与△EBF的相似比为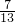 ,故D正确.
,故D正确.
故选C.
点评:本题考查了相似三角形的判定和性质、全等三角形的判定和性质以及垂直的定义,题目难度不大,但设计很新颖.
分析:根据全等三角形的判定和性质、相似三角形的判定和性质以及锐角三角函数逐项分析即可.
解答:∵ED⊥AC,
∴∠ADF=90°,
∴∠A+∠BFE=90°,
∵∠ABE=90°,
∴∠E+∠BFE=90°,
∴∠A=∠E,
∵在△ABC和△EBF中,
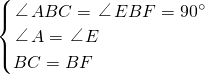 ,
,∴△ABC≌△EBF(AAS),故A正确;
∵sinA=
 ,AB=12,
,AB=12,∴BC=5,AC=13,

∵∠A=∠A,∠ASDF=∠ABC=90°,
∴△ADF∽ABC,
∴
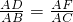 ,
,∵BC=BF,
∴BF=5,
∴AF=12-5=7,
∴
 =
=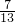 ,
,∴
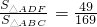 ,故B正确;
,故B正确;∵
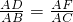 =
=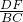 =
=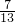 ,
,∴DF=
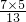 =
=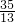 ,故C错误;
,故C错误;∵
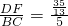 =
=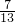 ,
,∴△ADF与△EBF的相似比为
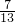 ,故D正确.
,故D正确.故选C.
点评:本题考查了相似三角形的判定和性质、全等三角形的判定和性质以及垂直的定义,题目难度不大,但设计很新颖.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.