题目内容
已知:△ABC的三边长分别为a,b,c,化简:|a-b+c|+|a-b-c|
考点:三角形三边关系,绝对值,整式的加减
专题:
分析:三角形三边满足的条件是,两边和大于第三边,两边的差小于第三边,根据此来确定绝对值内的式子的正负,从而化简计算即可.
解答:
解:∵△ABC的三边长分别是a、b、c,
∴必须满足两边之和大于第三边,两边的差小于第三边,则a-b+c>0,a-b-c<0,
∴|a-b+c|+|a-b-c|=a-b+c-a+b+c=2c.
∴必须满足两边之和大于第三边,两边的差小于第三边,则a-b+c>0,a-b-c<0,
∴|a-b+c|+|a-b-c|=a-b+c-a+b+c=2c.
点评:此题考查了三角形三边关系,此题的关键是先根据三角形三边的关系来判定绝对值内式子的正负.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
先观察下列三个等式,再回答下列问题.①
=1+
-
=1
;②
=1+
-
=1
;③
=1+
-
=1
,…,请你根据上面三个等式提供的信息,计算
的结果为( )
1+
|
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
1+
|
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
1+
|
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
1+
|
A、1
| ||
B、1
| ||
C、1
| ||
D、1
|
下列说法中,错误的是( )
| A、0的平方根是0 |
| B、1的平方根是1 |
| C、-1的立方根是-1 |
| D、负数没有平方根 |
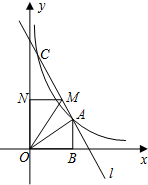 已知:如图,点A(2,m)在双曲线y=
已知:如图,点A(2,m)在双曲线y= 如图,做一个试管架,在长a cm的木条上钻4个圆孔,每个孔的半径均为2cm,则图中x为
如图,做一个试管架,在长a cm的木条上钻4个圆孔,每个孔的半径均为2cm,则图中x为 某校在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.小明同学根据获奖结果,绘制成如图所示的统计表和统计图.
某校在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.小明同学根据获奖结果,绘制成如图所示的统计表和统计图.