Question

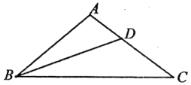
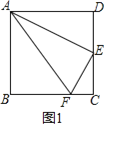
【题目】如图1，在正方形中，点是的中点，点是边上一点，且．

（1）求证：；

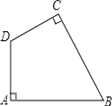
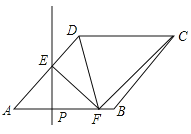
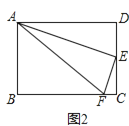
（2）将“正方形”改成“矩形”，其他条件均不变，如图2，你认为仍然有“”吗？若你同意，请以图2为例加以证明；若你不同意，请说明理由．

Answer 1

【答案】（1）见解析 （2）见解析

【解析】

(1)延长AE交BC的延长线于G点，如图1，由正方形性质得AD∥CG，∠D=∠BCD=∠DCG=90°，再证明△ADE≌△GCE得到AE=GE，∠DAE=∠G，接着证明FA=FG，然后根据等腰三角形的性质得到结论；
(2)延长AE交BC的延长线于G点，如图2，证明的方法与(1)一样，也可得到EF⊥AE．

(1)延长交的延长线于点，如图1，

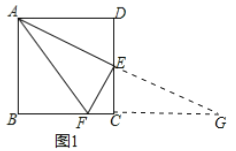
∵四边形是正方形，

∴，，

∵是的中点，

∴，

在和中，

，

∴，

∴，，

∵，

∴，

∴，

∴，即；

(2)仍然有“”，证明如下：

延长交的延长线于点，如图2，

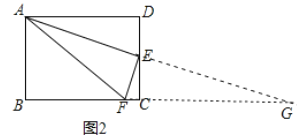
∵四边形是矩形，

∴，，

∵是的中点，

∴，

在和中，

，

∴，

∴，，

∵，

∴，

∴，

∴，即．