题目内容
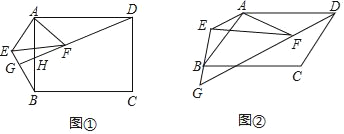
【题目】探究：如图①，在矩形ABCD中，以点A为直角顶点作Rt△AEF，连结BE、DF，直线DF交直线BE于点G，DG与AB交于点H，且
．
（1）求证：△ABE∽△ADF．
（2）求证：DG⊥BE；
拓展：如图②，在ABCD中，以点A为顶点作∠EAF＝∠BAD，连结BE、DF，直线DF交直线BE于点G，且，若∠BCD＝130°，则∠EGD的大小为 度．
【答案】（1）△ABE∽△ADF；（2）50．
【解析】
探究：（1）根据矩形的性质得到∠BAD=90°，根据余角的性质得到∠EAB=∠DAF，根据相似三角形的判定定理即可得到结论；
（2）根据相似三角形的性质得到∠ADF=∠ABE，根据对顶角相等得到∠AHD=∠BHG，根据三角形的内角和即可得到结论；拓展：根据平行四边形的性质得到AB∥CD，AD∥BC，求得∠ABC=180°-∠C=50°，∠ADF=∠2，根据相似三角形的性质得到∠ADF=∠3，根据三角形的内角和和平角的定义即可得到结论．
探究：（1）在矩形ABCD中，
∵∠BAD＝90°，
∵∠AEF＝90°，
∴∠EAB+∠BAF＝∠DAF+∠BAF＝90°，
∴∠EAB＝∠DAF，
∵
，
∴△ABE∽△ADF；
（2）∵△ABE∽△ADF，
∴∠ADF＝∠ABE，
设AB与DG的交点为H，
∵∠AHD＝∠BHG，
∴∠BGH＝180°﹣∠ABG﹣∠BHG＝180°﹣∠AHF﹣∠ADF＝∠BAD＝90°，
∴DG⊥BE；
拓展：在ABCD中，
∵AB∥CD，AD∥BC，
∴∠ABC＝180°﹣∠C＝50°，∠ADF＝∠2，
∵∠EAF＝∠BAD，
∴∠EAF﹣∠BAF＝∠BAD﹣∠BAF，
即∠EAB＝∠DAF，
∵，
∴△ABE∽△ADF，
∴∠ADF＝∠3，
∴∠2＝∠3，
∵∠ABC＝180°﹣∠GBC﹣∠3，∠EGD＝180°﹣∠GBD﹣∠2，
∴∠EGD＝∠ABC＝50°，
故答案为：50．
