题目内容
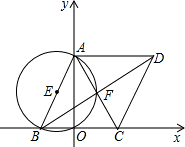 如图所示,在平面直角坐标系中,0为坐标原点,⊙E过点O.与x轴、y轴分别交于B、A两点,点E坐标为(-2,2
如图所示,在平面直角坐标系中,0为坐标原点,⊙E过点O.与x轴、y轴分别交于B、A两点,点E坐标为(-2,2 )F为弧A0的中点.点B,D关于F点成中心对称.
)F为弧A0的中点.点B,D关于F点成中心对称.
(1)求点c的坐标;
(2)点P从B点开始在折线段B-A-D上运动:点Q从B点开始在射线B0上运动,两点的运动速度均为2个长度单位每秒,设运动时间为t.△POQ的面积为y,求y与t之间的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,若y=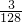 SABCD,求直线PQ与⊙E相交所得的弦长.
SABCD,求直线PQ与⊙E相交所得的弦长.
(1)解:过E作EM⊥OA于M,EN⊥OB于N,连接OE,
由勾股定理得:OE=4=AE=BE,
∴AB=8,∠BAO=30°,∠ABO=60°,OB=4,
∵AB是直径,
∴∠AFB=90°=∠BFC,
∵F为弧OA的中点,
∴∠ABF=∠CBF,
在△ABF和△CBF中
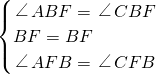 ,
,
∴△ABF≌△CBF,
∴AF=CF,∠ACB=∠ABC=60°,BC=AB=8,
∴OC=4,
∴C的坐标是(4,0)
(2)当Q在BO上时,P在AB上,
y= ×OQ×HOQ=
×OQ×HOQ= (4-2t)•
(4-2t)• t=-
t=- t2+2
t2+2 t(0<t<2);
t(0<t<2);
当Q在OC上时,P在AB上,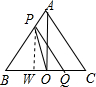
同法可求y= OQ×HOQ=
OQ×HOQ= ×(2t-4)×
×(2t-4)× t=
t= t2-2
t2-2 t(2<t≤4);
t(2<t≤4);
当Q在OC的延长线上时,
y= OQ×AO=
OQ×AO= ×(2t-4)×4
×(2t-4)×4 =4
=4 t-8
t-8 (4<t≤8);
(4<t≤8);
(3)S平行四边形ABCD=8×4 =32
=32 ,
,
①- t2+2
t2+2 t=
t=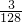 ×32
×32 ,
,
解得:t= 或
或
② t2-2
t2-2 t=
t=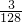 ×32
×32 ,
,
方程的解不在2<t≤4内,
③4 t-8
t-8 =
=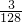 ×32
×32 ,
,
方程的解不在4<t≤8内,过E作EK⊥弦MN于K,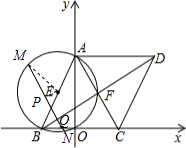
∴当t= 时,EP=4-
时,EP=4- ×2=3,∠EPM=60°,
×2=3,∠EPM=60°,
PK= ,EK=
,EK= ,
,
连接ME,由勾股定理得:MK=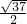 ,
,
弦MN=2MK=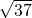 ;
;
当t= 时,
时,
同法可求弦长是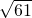 ;
;
分析:(1)过E作EM⊥OA于M,EN⊥OB于N,连接OE,根据圆周角定理求出∠ABF=∠CBF,∠AFB=∠CFB=90°,根据ASA证△ABF≌△CBF,求出AB=BC即可;
(2)分为三种情况:当Q在BO上时,P在AB上,当Q在OC的延长线上时,当Q在OC的延长线上时,根据三角形面积公式求出即可;
(3)求出平行四边形的面积,根据已知得出三个方程,求出方程的解,注意看是否在范围内,过E作EK⊥弦MN于K,求出EK、根据勾股定理求出MK即可;
点评:本题综合考查了圆周角定理、勾股定理、三角形的面积、点的坐标、全等三角形的性质和判定,垂径定理等知识点,此题是一道难度较大的题目,综合性比较强,对学生提出了较高的要求,分类讨论思想的运用.
由勾股定理得:OE=4=AE=BE,
∴AB=8,∠BAO=30°,∠ABO=60°,OB=4,
∵AB是直径,
∴∠AFB=90°=∠BFC,
∵F为弧OA的中点,
∴∠ABF=∠CBF,
在△ABF和△CBF中
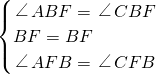 ,
,∴△ABF≌△CBF,
∴AF=CF,∠ACB=∠ABC=60°,BC=AB=8,
∴OC=4,
∴C的坐标是(4,0)
(2)当Q在BO上时,P在AB上,
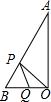
y=
 ×OQ×HOQ=
×OQ×HOQ= (4-2t)•
(4-2t)• t=-
t=- t2+2
t2+2 t(0<t<2);
t(0<t<2);当Q在OC上时,P在AB上,
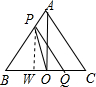
同法可求y=
 OQ×HOQ=
OQ×HOQ= ×(2t-4)×
×(2t-4)× t=
t= t2-2
t2-2 t(2<t≤4);
t(2<t≤4);当Q在OC的延长线上时,

y=
 OQ×AO=
OQ×AO= ×(2t-4)×4
×(2t-4)×4 =4
=4 t-8
t-8 (4<t≤8);
(4<t≤8);(3)S平行四边形ABCD=8×4
 =32
=32 ,
,①-
 t2+2
t2+2 t=
t=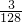 ×32
×32 ,
,解得:t=
 或
或
②
 t2-2
t2-2 t=
t=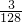 ×32
×32 ,
,方程的解不在2<t≤4内,
③4
 t-8
t-8 =
=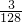 ×32
×32 ,
,方程的解不在4<t≤8内,过E作EK⊥弦MN于K,

∴当t=
 时,EP=4-
时,EP=4- ×2=3,∠EPM=60°,
×2=3,∠EPM=60°,PK=
 ,EK=
,EK= ,
,连接ME,由勾股定理得:MK=
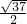 ,
,弦MN=2MK=
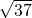 ;
;当t=
 时,
时,同法可求弦长是
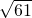 ;
;分析:(1)过E作EM⊥OA于M,EN⊥OB于N,连接OE,根据圆周角定理求出∠ABF=∠CBF,∠AFB=∠CFB=90°,根据ASA证△ABF≌△CBF,求出AB=BC即可;
(2)分为三种情况:当Q在BO上时,P在AB上,当Q在OC的延长线上时,当Q在OC的延长线上时,根据三角形面积公式求出即可;
(3)求出平行四边形的面积,根据已知得出三个方程,求出方程的解,注意看是否在范围内,过E作EK⊥弦MN于K,求出EK、根据勾股定理求出MK即可;
点评:本题综合考查了圆周角定理、勾股定理、三角形的面积、点的坐标、全等三角形的性质和判定,垂径定理等知识点,此题是一道难度较大的题目,综合性比较强,对学生提出了较高的要求,分类讨论思想的运用.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.
交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式. 5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )
5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )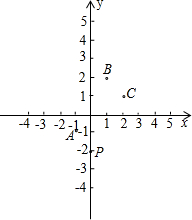 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去. 如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为
如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为 BE.
BE.