题目内容
如图, △ABC的三边分别为AC=5，BC=12，AB=13, 将△ABC沿AD折叠，使AC落在AB上.与E点重合。
（1）试判断△ABC的形状，并说明理由.
（2）求折痕AD的长.
【答案】
（１）证明出△ABC是直角三角形
（２）求出CD=
，AD=
【解析】解：（1）△ABC是直角三角形；
∵AC2+BC2=
=169=AB2，
∴∠C=90°；
∴△ABC是直角三角形．
（2）设折叠后点C与AB上的点E重合．
设CD=x，则DE=x，AE=5，BE=8，BD=12-x；
∵∠AED=∠C=90°，
∴在Rt△EBD中，x2+82=（12-x）2，
解得：x= ，
∴AD=
练习册系列答案
相关题目
18、如图，△ABC的三个内角大小分别为x，x，3x，则x的值为（ ）
如图，△ABC的三个顶点A、B、C的坐标分别为（3，3）、（6，4）（4，6），则BC边上的高为
如图，△ABC的三个顶点分别在正方形网格的格点上，则tan∠C的值是（ ）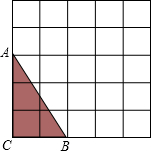
（2012•漳州模拟）如图，△ABC的三个顶点都在5×5的网格（每个小正方形的边长均为1个单位长度）的格点上．
21、如图，△ABC的三个顶点坐标分别为A（-3，-3），B（-1，-2），