Question

△ABC中，AD是边BC上的高，如果AD²=BD•DC，那么△ABC是________三角形（按角分类）．

Answer 1

直角或钝角
分析：当点D在△ABC内时，先根据AD是高，则△ABD及△ACD是直角三角形，再根据AD²=BD•CD及勾股定理的逆定理可得出AB²+AC²=BC²，即∠BAC=90°；当点D在△ABC外时，由三角形内角与外角的关系可知，则∠ACB＞90°，故△ABC是直角或钝角三角形．
解答：如图（1），由AD²=BD•CD，
有AB²+AC²=BD²+CD²+2AD²=BD²+CD²+2BD•DC=（BD+CD）²，

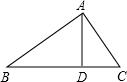
即AB²+AC²=BC²，
可得∠BAC=90°，
如图（2），虽然AD²=BD•CD，D点在△ABC外，
则∠ACB＞90°，
∴△ABC是直角或钝角三角形．

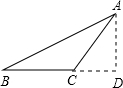
故答案为：直角或钝角．
点评：本题考查的是相似三角形的判定与性质，勾股定理的逆定理，解答此题时要分AD在△ABC内和在△ABC内两种情况讨论．