Question

已知，三个直径分别为2，4，5的图如图排列，每两个圆之间外切，O₁P切⊙O₃于点P，则图中阴影部分面积为

4

3

π-

3

．

Answer 1

分析：连接O₁O₃，O₃P，设直线O₁P交⊙O₂于A、B，连接O₂A，O₂B，过O₂作O₂C⊥AB于C，推出△O₁CO₂∽△O₁PO₃，得出

O2C

O3P

=

O1O2

O1O3

，代入求出O₂C=1，由勾股定理求出BC=

3

，由垂径定理求出AB=2BC=2

3

，求出∠CBO₂=30°，求出∠AO₂B=120°，根据S=S 扇形AO2B-S △AO2B求出即可．

解答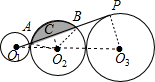：解：连接O₁O₃，O₃P，设直线O₁P交⊙O₂于A、B，连接O₂A，O₂B，过O₂作O₂C⊥AB于C，
∵O₁P切⊙O₃于P，
∴O₃P⊥O₁P，
∴O₂C∥O₃P，
∴△O₁CO₂∽△O₁PO₃，
∴

O2C

O3P

=

O1O2

O1O3

，
∴

O2C

5 2

=

1+2

1+4+ 5 2

，
∴O₂C=1，
由勾股定理得：BC=

22-12

=

3

，
∵O₂C⊥AB，O₂C过圆心O₂，
∴AB=2BC=2

3

，
∵O₂B=2=2O₂C，∠O₂CB=90°，
∴∠CBO₂=30°，
∴∠CO₂B=60°，
∵AO₂=BO₂，O₂C⊥AB，
∴∠AO₂C=∠BO₂C=60°，
∴∠AO₂B=60°+60°=120°，
∴阴影部分的面积S=S 扇形AO2B-S △AO2B=

120π×22

360

-

1

2

×2

3

×1=

4

3

π-

3

，
故答案为：

4

3

π-

3

．

点评：本题考查了切线的性质，两圆相切的性质，相似三角形的性质和判定，求扇形的面积，含30度角的直角三角形性质，勾股定理等知识点的综合运用，主要考查学生的推理和计算的能力．