题目内容
若(2x-1)3=a+bx+cx2+dx3,要求a+b+c+d的值,可令x=1,原等式变形为: ,
所以,a+b+c+d= .
想一想:利用上述求a+b+c+d的方法,能否求:
(1)a的值;
(2)a+c的值?若能,写出解答过程,若不能,说明理由.
所以,a+b+c+d=
想一想:利用上述求a+b+c+d的方法,能否求:
(1)a的值;
(2)a+c的值?若能,写出解答过程,若不能,说明理由.
考点:代数式求值
专题:计算题
分析:(1)令x=0即可确定出a的值;
(2)令x=-1得到关系式,与a+b+c+d的值联立求出a的值即可.
(2)令x=-1得到关系式,与a+b+c+d的值联立求出a的值即可.
解答:解:原式变形为(2-1)3=a+b+c+d;即a+b+c+d=1;
(1)令x=0得:a=-1;
(2)令x=-1得:a-b+c-d=-27,
又a+b+c+d=1,
则a+c=-13.
故答案为:(2-1)3=a+b+c+d;1
(1)令x=0得:a=-1;
(2)令x=-1得:a-b+c-d=-27,
又a+b+c+d=1,
则a+c=-13.
故答案为:(2-1)3=a+b+c+d;1
点评:此题考查了代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
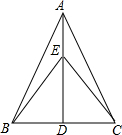 已知如图,AB=AC,AD平分∠BAC,E是AD上一点,求证:
已知如图,AB=AC,AD平分∠BAC,E是AD上一点,求证: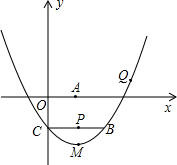 如图,过点C(0,-2)的抛物线y=ax2+bx+c的顶点M坐标为(2,-3),过点C作CB∥x轴交抛物线于点B,点P在线段BC上,CP=m.
如图,过点C(0,-2)的抛物线y=ax2+bx+c的顶点M坐标为(2,-3),过点C作CB∥x轴交抛物线于点B,点P在线段BC上,CP=m.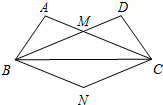 如图,在△ABC和△DCB中,AC=BD,AB=CD,AC、BD交于点M.
如图,在△ABC和△DCB中,AC=BD,AB=CD,AC、BD交于点M.