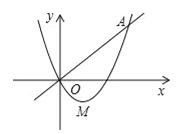
题目内容
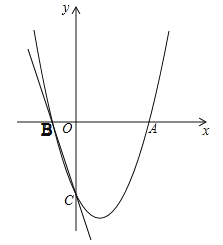
【题目】如图,将二次函数![]() (其中
(其中![]() )的图象在
)的图象在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,形成新的图象记为
轴翻折,图象的其余部分保持不变,形成新的图象记为![]() ,另有一次函数
,另有一次函数![]() 的图象记为
的图象记为![]() ,若
,若![]() 与
与![]() 恰有两个交点时,则
恰有两个交点时,则![]() 的范围是________.
的范围是________.
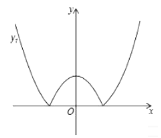
【答案】![]() 或
或![]()
【解析】
根据题意得出翻折后的抛物线解析式为![]() ,若
,若![]() 与
与![]() 恰有两个交点,则需分两种情况,①当直线与
恰有两个交点,则需分两种情况,①当直线与![]() 和
和![]() 分别有一个交点时,结合图象即可解答;②当直线与
分别有一个交点时,结合图象即可解答;②当直线与![]() 有两个交点,直线与
有两个交点,直线与![]() 无交点时,联立方程组,利用根的判别式求出m的值,结合图象即可解答.
无交点时,联立方程组,利用根的判别式求出m的值,结合图象即可解答.
解:二次函数![]() (其中
(其中![]() )的图象在
)的图象在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折得到的抛物线解析式为:
轴翻折得到的抛物线解析式为:![]() ,
,
∵直线![]() ,
,
当x=0时,y=2,当y=0时,x=-2,
∴直线![]() 与x轴交点为(-2,0),与y轴的交点为(0,2),
与x轴交点为(-2,0),与y轴的交点为(0,2),
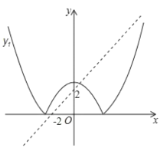
①如下图,当抛物线经过点(-2,0)时,0=4-m,解得m=4,
观察图象可知,当m>4时,![]() 与
与![]() 恰有两个交点,
恰有两个交点,
②由![]() 得
得![]() ,当
,当![]() 时,解得:
时,解得:![]() ,
,
观察图象可知,当![]() 时,
时,![]() 与
与![]() 恰有两个交点,
恰有两个交点,
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目