题目内容
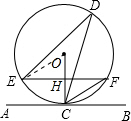
 如图,直线AB切⊙O于C点,D是⊙O上的一点,∠EDC=30°,弦EF∥AB,连接OC交EF于H点,连接CF,CF=2.
如图,直线AB切⊙O于C点,D是⊙O上的一点,∠EDC=30°,弦EF∥AB,连接OC交EF于H点,连接CF,CF=2.求:(1)CH的长;
(2)⊙O的半径.
分析:(1)根据圆周角定理可得∠CFH=∠EDC=30°,继而在Rt△CHF中可求出CH的长;
(2)连接OE,设半径为r,则可表示出OE=r,也可表示出OH,在Rt△OEH中利用勾股定理可求出r.
(2)连接OE,设半径为r,则可表示出OE=r,也可表示出OH,在Rt△OEH中利用勾股定理可求出r.
解答:解:(1)∵AB是直线AB切⊙O于C点,
∴OC⊥AB,
又∵EF∥AB,
∴OC⊥EF,
∵∠EDC=30°,
∴∠CFH=∠EDC=30°(圆周角定理),
在Rt△CHF中,CH=
CF=1;
(2)连接OE,
∵CH=1,∠CFH=30°,
∴HF=
,
∴EH=HF=
(垂径定理),
设⊙O的半径为r,则OE=r,OH=r-1,
在Rt△OEH中,r2=(
)2+(r-1)2,
解得:r=2.
故⊙O的半径为2.
∴OC⊥AB,
又∵EF∥AB,
∴OC⊥EF,
∵∠EDC=30°,
∴∠CFH=∠EDC=30°(圆周角定理),
在Rt△CHF中,CH=
| 1 |
| 2 |
(2)连接OE,

∵CH=1,∠CFH=30°,
∴HF=
| 3 |
∴EH=HF=
| 3 |
设⊙O的半径为r,则OE=r,OH=r-1,
在Rt△OEH中,r2=(
| 3 |
解得:r=2.
故⊙O的半径为2.
点评:本题考查了切线的性质、圆周角定理及含30°角的直角三角形的性质,综合考察的知识点较多,难度一般,注意各知识点的掌握.

练习册系列答案
相关题目
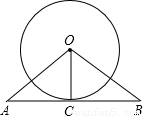
 10、如图,直线AB切⊙O于点C,∠OAC=∠OBC,则下列结论错误的是( )
10、如图,直线AB切⊙O于点C,∠OAC=∠OBC,则下列结论错误的是( ) 1、如图,直线AB切⊙O于点A,割线BDC交⊙O于点D、C.若∠C=30°,∠B=20°,则∠ADC=( )
1、如图,直线AB切⊙O于点A,割线BDC交⊙O于点D、C.若∠C=30°,∠B=20°,则∠ADC=( )