题目内容
【题目】如图,抛物线![]()
![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ,抛物线的对称轴为
,抛物线的对称轴为![]() .
.
(1)求抛物线的解析式;
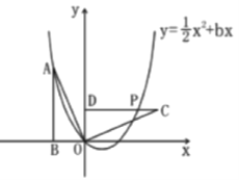
(2)如图1,对称轴上是否存在点![]() ,使
,使![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
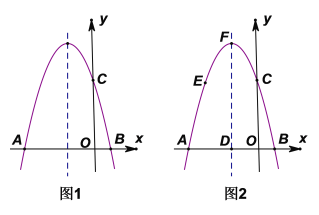
(3)如图2,抛物线的顶点为![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]() ,点
,点![]() 为抛物线上一点,点
为抛物线上一点,点![]() 不与点
不与点![]() 重合. 当
重合. 当![]() 时,过点
时,过点![]() 分别作
分别作![]() 轴的垂线和平行线,与
轴的垂线和平行线,与![]() 轴交于点
轴交于点![]() 、与对称轴交于点
、与对称轴交于点![]() ,得到矩形
,得到矩形![]() ,求矩形
,求矩形![]() 周长的最大值;
周长的最大值;
【答案】(1) ![]() ,(2) 存在,
,(2) 存在,![]() ,
,![]() ; (3)
; (3) ![]()
【解析】
(1)根据抛物线的对称轴方程以及A、B的距离得到![]() 、
、![]() 两点的坐标,再根据很熟的开口方向即可得到函数的解析式;
两点的坐标,再根据很熟的开口方向即可得到函数的解析式;
(2) 根据![]() 中,
中,![]() 以及
以及![]() ,
,![]() 得到
得到![]() 则
则![]() 的垂直平分线与对称轴的交点即为
的垂直平分线与对称轴的交点即为![]() 点,求解即可得到P点坐标;
点,求解即可得到P点坐标;
(3)分情况①![]() 时,以及②
时,以及②![]() 讨论,根据
讨论,根据![]() 分别计算,利用二次函数的性质即可得到答案;
分别计算,利用二次函数的性质即可得到答案;
解:(1) ∵抛物线![]()
![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() 两点,且
两点,且 ![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ,抛物线的对称轴为
,抛物线的对称轴为![]() ,
,
∴![]() ,
,![]() ,
,
又∵函数开口向下,
∴抛物线的解析式;![]() ;
;
(2)![]() 中,
中,![]() ,
,
∵![]() ,
,![]()
∴![]()
则如图:
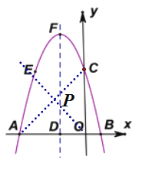
则![]() 的垂直平分线与对称轴的交点即为
的垂直平分线与对称轴的交点即为![]() 点,
点,
又∵对称轴的方程为:![]() ,
,
∴P点到x轴的距离也是3,即PD=3,
又∵P在第二象限,
∴![]() ,
,![]() ;
;
(3)设![]()
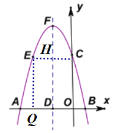
①![]() 时,
时,
![]()
即:![]()
当![]() 时,
时,![]() ;
;
②![]() 时,
时,
![]()
![]()
当![]() 时,
时,![]() ;
;

 阅读快车系列答案
阅读快车系列答案【题目】现在,步行运动深受广大健身爱好者的喜爱. 通过“微信运动”可以查询微信好友当天的行走步数.实验中学张老师根据该校![]() 名教师某日“微信运动”中的行走步数,绘制成如下两张统计表(不完整).
名教师某日“微信运动”中的行走步数,绘制成如下两张统计表(不完整).
步数 | 频数 | 频率 |
|
| 0.2 |
| 19 | 0.38 |
|
| 0.3 |
| 4 |
|
| 2 | 0.04 |
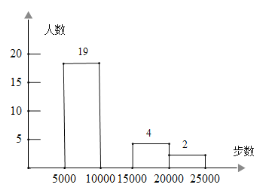
(1)写出左表中![]() 、
、![]() 、
、![]() 的值,并补全条形统计图;
的值,并补全条形统计图;
(2)实验中学所在的某县有![]() 名教师,用张老师调查的样本数据估计该县当天行走步数不少于
名教师,用张老师调查的样本数据估计该县当天行走步数不少于![]() 步的教师有多少人?
步的教师有多少人?
(3)在该校![]() 名教师中,随机选取当天行走步数不少于
名教师中,随机选取当天行走步数不少于![]() 步的
步的![]() 名教师参加“我运动,我健康”的征文活动,求选中的
名教师参加“我运动,我健康”的征文活动,求选中的![]() 名教师的行走步数都不小于
名教师的行走步数都不小于![]() 步的概率.
步的概率.