��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���m��n����mn=k��kΪ��������m��0��n��0��ʱ���ͳƵ㣨m��n��Ϊ���Ȼ��㡱��
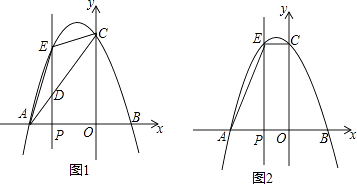
��1����k=4������y=x��4��ͼ�������������ģ����Ȼ��㡱���ꣻ
��2����ֱ��y=��x+b��b��0����x�ᡢy��ֱ��ڵ�A�͵�B������ֱ������ֻ��һ�����Ȼ��㡱������A��y��ƽ�е�ֱ�ߺ���B��x��ƽ�е�ֱ�߽��ڵ�C����E��ֱ��AC�ϵġ��Ȼ��㡱����F��ֱ��BC�ϵġ��Ȼ��㡱������OEF�����Ϊk2+ ![]() k��
k�� ![]() ����EF��ֵ��
����EF��ֵ��
���𰸡�
��1��
�⣺�衰�Ȼ��㡱����Ϊ��m��n�������� ![]() ���
��� ![]() ��
�� ![]() ����������
����������
�ࡰ�Ȼ��㡱����Ϊ��2 ![]() +2��2
+2��2 ![]() ��2��
��2��
��2��
�⣺��ͼ�������⡰�Ȼ��㡱�ڷ���������y= ![]() ͼ���ϣ�
ͼ���ϣ�

��ֱ��y=��x+b��b��0����x�ᡢy��ֱ��ڵ�A�͵�B������ֱ������ֻ��һ�����Ȼ��㡱��
�ࡰ�Ȼ��㡱M������Ϊ�� ![]() ��
�� ![]() ����B��0��2
����B��0��2 ![]() ����A��2
����A��2 ![]() ��0����E��2
��0����E��2 ![]() ��
�� ![]()
![]() ����F��
����F�� ![]()
![]() ��2
��2 ![]() ����
����
�ߡ�OEF�����=S������AOBC��2S��AOE��S��EFC=k2+ ![]() k��
k�� ![]() ��
��
��k2+ ![]() k��
k�� ![]() =4k��k��
=4k��k�� ![]() k��
k��
���k=1�� ![]() ����������
����������
��E��2�� ![]() ����F��
����F�� ![]() ��2����
��2����
��EF= ![]() =
= ![]()
![]()
����������1���衰�Ȼ��㡱����Ϊ��m��n�������� ![]() �ⷽ���鼴�ɣ���2����ͼ�������⡰�Ȼ��㡱�ڷ���������y=
�ⷽ���鼴�ɣ���2����ͼ�������⡰�Ȼ��㡱�ڷ���������y= ![]() ͼ���ϣ�ֱ��y=��x+b��b��0����x�ᡢy��ֱ��ڵ�A�͵�B������ֱ������ֻ��һ�����Ȼ��㡱�����ԡ��Ȼ��㡱M������Ϊ��
ͼ���ϣ�ֱ��y=��x+b��b��0����x�ᡢy��ֱ��ڵ�A�͵�B������ֱ������ֻ��һ�����Ȼ��㡱�����ԡ��Ȼ��㡱M������Ϊ�� ![]() ��
�� ![]() ����B��0��2
����B��0��2 ![]() ����A��2
����A��2 ![]() ��0����E��2
��0����E��2 ![]() ��
�� ![]()
![]() ����F��
����F�� ![]()
![]() ��2
��2 ![]() �������ݡ�OEF�����=S������AOBC��2S��AOE��S��EFC=k2+
�������ݡ�OEF�����=S������AOBC��2S��AOE��S��EFC=k2+ ![]() k��
k�� ![]() ���г����̼��ɽ�����⣮
���г����̼��ɽ�����⣮
�����㾫��������һ�κ��������ʺ�һ�κ����ĸ����ǽ����ĸ�������Ҫ֪��һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С��һ��أ����y=kx+b��k��b�dz�����k������0������ôy����x��һ�κ�����