题目内容
已知△ABC≌△A′B′C′,且∠A=48°,∠B=33°,A′B′=5cm,求∠C′的度数与AB的长.
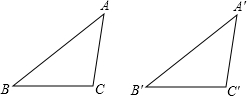 解:∵∠A=48°,∠B=33°,
解:∵∠A=48°,∠B=33°,∴∠C=180°-∠A-∠B=180°-48°-33°=180°-81°=99°,
∵△ABC≌△A′B′C′,A′B′=5cm,
∴∠C′=∠C=99°,AB=A′B′=5厘米.
分析:根据三角形的内角和等于180°求出∠C,然后根据全等三角形对应角相等,全等三角形对应边相等解答即可.
点评:本题考查了全等三角形的性质,三角形的内角和定理,根据全等三角形对应字母放在对应位置上准确找出对应角与对应边是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
已知ABC的三边满足a2+b2+c2-ab-bc-ac=0,则这个三角形的形状是( )
| A、直角三角形 | B、等腰三角形 | C、等腰直角三角形 | D、等边三角形 |
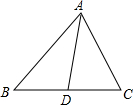 如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )
如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )| A、3<AD<4 | ||||
| B、1<AD<7 | ||||
C、
| ||||
D、
|
已知△ABC中,cosA=
,tgB=1,则△ABC的形状是( )
| 1 |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
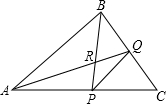 如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于
如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于