题目内容
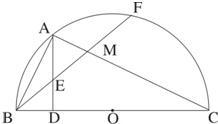 19、如图,已知BC是半圆O的直径,AB=AF,AC与BF交于点M,AD⊥BC于D,交BF于E,求证BE=EM.
19、如图,已知BC是半圆O的直径,AB=AF,AC与BF交于点M,AD⊥BC于D,交BF于E,求证BE=EM.分析:此题可以借助中间线段AE,分别证明AE=BE,AE=ME.首先根据等弦对等弧,得到弧AB=弧AF.再根据直径所对的圆周角是直角和等角的余角相等,证明∠BAE=∠C.再根据等弧所对的圆周角相等,得到∠ABE=∠C.从而证明∠ABE=∠BAE,再根据等角的余角相等得到∠EAM=∠AME.
解答:证明:∵弧AB=弧AF,
∴∠ACB=∠ABF.
∵BC是直径,
∴∠BAC=90°.
又AD⊥BC,
∴∠BAD+∠DAC=90°,∠ACB+∠DAC=90°.
∴∠BAD=∠ACB.
∴∠BAD=∠ABF.
∴AE=BE.
∵∠BAM=90°,
∴∠BAD+∠DAC=90°,∠ABF+∠AMB=90°.
∴∠DAC=∠AMB.
∴EM=EA.
∴BE=EM.
∴∠ACB=∠ABF.
∵BC是直径,
∴∠BAC=90°.
又AD⊥BC,
∴∠BAD+∠DAC=90°,∠ACB+∠DAC=90°.
∴∠BAD=∠ACB.
∴∠BAD=∠ABF.
∴AE=BE.
∵∠BAM=90°,
∴∠BAD+∠DAC=90°,∠ABF+∠AMB=90°.
∴∠DAC=∠AMB.
∴EM=EA.
∴BE=EM.
点评:此题综合运用了圆周角定理的推论、等弧对等弦、等角的余角相等以及等角对对边的性质.

练习册系列答案
相关题目
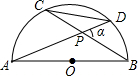 如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,那么CD:AB等于( )
如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,那么CD:AB等于( )| A、sinα | ||
| B、cosα | ||
| C、tanα | ||
D、
|



