题目内容
如图所示,在梯形ABCD中,AB∥CD,E是BC的中点,EF⊥AD于点F,AD=4,EF=5,则梯形ABCD的面积是 .
【答案】分析:作延长DE交AB延长线上点H,过点H作HM⊥FE,交FE的延长线上于点H,然后将梯形ABCD的面积转化为梯形HMFA的面积,即可求解.
解答:解:延长DE交AB延长线上点H,过点H作HM⊥FE,交FE的延长线上于点M,

∵CD∥AB,E是BC中点,
∴∠EBH=∠C,CE=BE,
在△DCE和△HBE中, ,
,
∴△DCE≌△HBE,
∴DE=EH,即点E也是DH的中点,
∵∠M=∠DFE=90°,
∴MH∥AD,
在△DEF和△HEM中,
∴△DEF≌△HEM,
∴HM=DF,EM=EF=5,
∴HM+AF=DF+AF=AD=4,FM=FE+EM=2EF=10,
∴梯形ABCD与梯形HMFA的面积相等,
S梯形HMFA= (HM+AF)×FM=
(HM+AF)×FM= ×4×10=20.
×4×10=20.
故答案为:20.
点评:本题考查了梯形的知识,关键是利用全等三角形的判定把梯形ABCD的面积转化为梯形AFMH的面积,要求熟练全等三角形的判定定理,难度较大.
解答:解:延长DE交AB延长线上点H,过点H作HM⊥FE,交FE的延长线上于点M,

∵CD∥AB,E是BC中点,
∴∠EBH=∠C,CE=BE,
在△DCE和△HBE中,
 ,
,∴△DCE≌△HBE,
∴DE=EH,即点E也是DH的中点,
∵∠M=∠DFE=90°,
∴MH∥AD,
在△DEF和△HEM中,

∴△DEF≌△HEM,
∴HM=DF,EM=EF=5,
∴HM+AF=DF+AF=AD=4,FM=FE+EM=2EF=10,
∴梯形ABCD与梯形HMFA的面积相等,
S梯形HMFA=
 (HM+AF)×FM=
(HM+AF)×FM= ×4×10=20.
×4×10=20.故答案为:20.
点评:本题考查了梯形的知识,关键是利用全等三角形的判定把梯形ABCD的面积转化为梯形AFMH的面积,要求熟练全等三角形的判定定理,难度较大.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
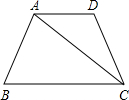 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.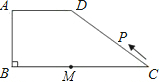 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有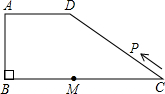 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.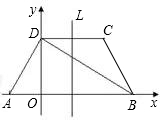 如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是
如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是 如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )
如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )