题目内容
 某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C).
某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C).
(1)求y与x之间的函数关系.
(2)若果园种植该水果的成本是2800元/吨,那么公司本次采购量为多少时,果园在这次买卖中所获利润最大?最大利润是多少?
解:(1)当0<x≤20时,y=8000,
当20<x≤40时,设y=kx+b,
将点(20,8000)、(40,4000)代入可得: ,
,
解得: ,
,
故此时y=-200x+12000,
综上可得y=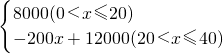 ;
;
(2)当0<x≤20时,w利润=(8000-2800)x=5200x,
当x=20时,w取得最大,w最大=104000元;
当20<x≤40时,w利润=(-200x+12000-2800)x=-200x2+9200x=-200(x-23)2+105800,
当x=23时,w利润取得最大,w最大=105800元;
综上可得公司本次采购量为23吨时,果园在这次买卖中所获利润最大,最大利润是105800元.
分析:(1)结合函数图象,讨论x的范围,分别得出y与x的函数关系式即可;
(2)分段表示出利润,各自求出最大值,然后综合即可得出采购量.
点评:本题考查了二次函数的应用,涉及了待定系数法求函数解析式的知识,解答本题的关键是将x的范围分段讨论,这也是本题的难点.
当20<x≤40时,设y=kx+b,
将点(20,8000)、(40,4000)代入可得:
 ,
,解得:
 ,
,故此时y=-200x+12000,
综上可得y=
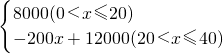 ;
;(2)当0<x≤20时,w利润=(8000-2800)x=5200x,
当x=20时,w取得最大,w最大=104000元;
当20<x≤40时,w利润=(-200x+12000-2800)x=-200x2+9200x=-200(x-23)2+105800,
当x=23时,w利润取得最大,w最大=105800元;
综上可得公司本次采购量为23吨时,果园在这次买卖中所获利润最大,最大利润是105800元.
分析:(1)结合函数图象,讨论x的范围,分别得出y与x的函数关系式即可;
(2)分段表示出利润,各自求出最大值,然后综合即可得出采购量.
点评:本题考查了二次函数的应用,涉及了待定系数法求函数解析式的知识,解答本题的关键是将x的范围分段讨论,这也是本题的难点.

练习册系列答案
相关题目
为喜迎佳节,沙坪坝区某食品公司推出一种新年礼盒,每盒成本为20元.在元旦节前30天进行销售后发现,该礼盒在这30天内的日销售量p(盒)与时间x(天)的关系如下表:
| 时间x(天) | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | … |
| 日销售量p(盒) | 78 | 76 | 74 | 72 | 70 | … |
 (1≤x≤20,且x为整数),后10天每天的销售价格y2(元/盒)与时间x(天)的函数关系式为
(1≤x≤20,且x为整数),后10天每天的销售价格y2(元/盒)与时间x(天)的函数关系式为 (21≤x≤30,且x为整数).
(21≤x≤30,且x为整数).(1)直接写出日销售量p(盒)与时间x(天)之间的关系式;
(2)请求出这30天中哪一天的日销售利润最大?最大日销售利润是多少?
(3)元旦放假期间,该公司采取降价促销策略.元旦节当天,销售价格(元/盒)比第30天的销售价格降低a%,而日销售量就比第30天提高了4a%,日销售利润比前30天中的最大日销售利润少380元,求a的值.
注:销售利润=(售价-成本价)×销售量.