题目内容
若正比例函数y=kx（k≠0）经过点（-1，2），则k的值为________．
-2
分析：根据正比例函数图象上点的坐标特征，将点（-1，2）代入正比例函数y=kx（k≠0），列出关于k的方程，然后解方程即可．
解答：∵正比例函数y=kx（k≠0）经过点（-1，2），
∴点（-1，2）满足正比例函数y=kx（k≠0），
∴2=-k，
解得，k=-2；
故答案是：-2．
点评：本题考查了待定系数法求正比例函数解析式．解题时，利用了正比例函数图象上点的坐标特征，函数图象上的点的坐标都满足该函数的解析式．
分析：根据正比例函数图象上点的坐标特征，将点（-1，2）代入正比例函数y=kx（k≠0），列出关于k的方程，然后解方程即可．
解答：∵正比例函数y=kx（k≠0）经过点（-1，2），
∴点（-1，2）满足正比例函数y=kx（k≠0），
∴2=-k，
解得，k=-2；
故答案是：-2．
点评：本题考查了待定系数法求正比例函数解析式．解题时，利用了正比例函数图象上点的坐标特征，函数图象上的点的坐标都满足该函数的解析式．
练习册系列答案
相关题目
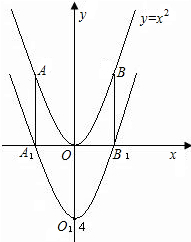与y轴的交点为O1，A1、B1、O1对应y=x2上的点依次为A、B、O．
如图，已知一次函数y=-x+2的图象与x轴交于点A，与y轴交于点C．