题目内容
 如图,已知一次函数y=-x+2的图象与x轴交于点A,与y轴交于点C.
如图,已知一次函数y=-x+2的图象与x轴交于点A,与y轴交于点C.(1)求∠CAO的度数;
(2)若将直线y=-x+2沿x轴向右平移两个单位,试求出平移后的直线的解析式;
(3)若正比例函数y=kx(k≠0)的图象与y=-x+2的图象交于点B,且∠ABO=30°,求AB的长及点B的坐标.
分析:(1)对于一次函数解析式,分别令y与x为0,求出对应x与y的值,确定出A与C坐标,得到AO=CO,即三角形AOC为等腰直角三角形,利用等腰直角三角形的性质即可求出∠CAO的度数;
(2)利用平移规律:“左加右减”,即可确定出平移后的直线解析式;
(3)根据题意画出图形,利用锐角三角函数关系以及30°所对的边等于斜边的一半,得出AB的长,进而即可求出B的坐标,进而求出AB的长.
(2)利用平移规律:“左加右减”,即可确定出平移后的直线解析式;
(3)根据题意画出图形,利用锐角三角函数关系以及30°所对的边等于斜边的一半,得出AB的长,进而即可求出B的坐标,进而求出AB的长.
解答:解:(1)对于一次函数y=-x+2,
令x=0,求出y=2;令y=0,求出x=2,
∴A(2,0),C(0,2),即OA=OC=2,
∴△AOC为等腰直角三角形,
∴∠CAO=45°;
(2)利用平移规律得:平移后的直线解析式为y=-(x-2)+2=-x+4;

(3)根据题意画出相应的图形,过O作OD⊥AB,于点D,
∵一次函数y=-x+2的图象与x轴交于点A,与y轴交于点C,
∴可求出A(2,0),C(0,2),
∴Rt△AOC是等腰直角,
∴DO=CD=AD,
∵CO=OA=2,
∴CD=DO=AD=
,
在△DOB中,∠DBO=30°,
∴BO=2
,
∴BD=
=
,
∴AB=
+
,
∴B点纵坐标为:
=
+1,
∴B点横坐标为:-[(
+1)-2]=1-
,
∴B(1-
,1+
),
同理可得出:AB′=
-
,
∴B′点横坐标为:
+2=
+1,
B′点纵坐标为:-
=-
+1,
∴B′(1+
,1-
).
令x=0,求出y=2;令y=0,求出x=2,
∴A(2,0),C(0,2),即OA=OC=2,
∴△AOC为等腰直角三角形,
∴∠CAO=45°;
(2)利用平移规律得:平移后的直线解析式为y=-(x-2)+2=-x+4;

(3)根据题意画出相应的图形,过O作OD⊥AB,于点D,
∵一次函数y=-x+2的图象与x轴交于点A,与y轴交于点C,
∴可求出A(2,0),C(0,2),
∴Rt△AOC是等腰直角,
∴DO=CD=AD,
∵CO=OA=2,
∴CD=DO=AD=
| 2 |
在△DOB中,∠DBO=30°,
∴BO=2
| 2 |
∴BD=
(2
|
| 6 |
∴AB=
| 6 |
| 2 |
∴B点纵坐标为:
| ||||
|
| 3 |
∴B点横坐标为:-[(
| 3 |
| 3 |
∴B(1-
| 3 |
| 3 |
同理可得出:AB′=
| 6 |
| 2 |
∴B′点横坐标为:
| ||||
|
| 3 |
B′点纵坐标为:-
| ||||
|
| 3 |
∴B′(1+
| 3 |
| 3 |
点评:此题考查了一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,等腰直角三角形的判定与性质,两直线的交点坐标,以及平移规律,确定出直线OB解析式是解第三问的关键.

练习册系列答案
相关题目
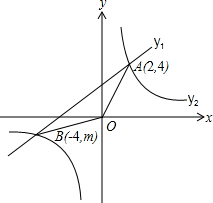 B(-4,m)两点.
B(-4,m)两点. 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数