题目内容
如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.小明的一种设计方案是:如图,在扇形纸片OAB内,画正方形CDEF,使C、D在OA上,F在OB上;连接OE并延长交弧AB于I,画IH∥ED交OA于H,IJ∥EF交OB于J,再画JG∥FC交OA于G.
(1)你能说明
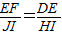 吗?
吗?(2)四边形GHIJ是正方形吗?如果是,请证明.如果不是,请说明理由.
(3)如果扇形OAB的圆心角∠AOB=30°,OA=6cm,小明截得的四边形GHIJ面积是多少(
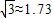 ,结果精确到0.1cm2)?
,结果精确到0.1cm2)?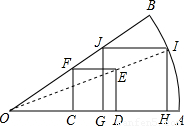
【答案】分析:(1)根据平行线分线段成比例定理推出比例式(都等于 ),推出即可;
),推出即可;
(2)证出四边形GHIJ是平行四边形,推出J=HI,∠IHG=90°,根据正方形的定义求出即可;
(3)设正方形GHIJ的边长为x,推出GH=HI=JG=x,根据∠GOJ=30°求出OG= ,OH=
,OH= +x,根据勾股定理得出OI2=OH2+HI2,代入求出即可.
+x,根据勾股定理得出OI2=OH2+HI2,代入求出即可.
解答:(1)证明:∵IJ∥EF,IH∥ED,
∴ ,
, ,
,
∴ .
.
(2)四边形GHIJ是正方形,
证明:∵CDEF是正方形,
∴EF=DE=CD=CF,
∵ =
= ,
,
∴JI=HI,
∵IH∥ED,IJ∥EF,JG∥FC,
∴IJ∥DH,IH∥JG,∠IHG=∠EDC=90°,
∴四边形GHIJ是正方形.
(3)解:设正方形GHIJ的边长为x,则GH=HI=JG=x,在直角三角形△OGJ,∠GOJ=30°,
∴OG= ,OH=
,OH= +x,∵OI2=OH2+HI2,
+x,∵OI2=OH2+HI2,
∴ ,
,
解得: ,
,
∴正方形GHIJ的面积是4.3cm2.
点评:本题考查了正方形的性质和判定,勾股定理,平行线分线段成比例定理等知识点的应用,关键是证出正方形GHIJ和根据含30度的直角三角形的性质得出方程,题目比较典型.
 ),推出即可;
),推出即可;(2)证出四边形GHIJ是平行四边形,推出J=HI,∠IHG=90°,根据正方形的定义求出即可;
(3)设正方形GHIJ的边长为x,推出GH=HI=JG=x,根据∠GOJ=30°求出OG=
 ,OH=
,OH= +x,根据勾股定理得出OI2=OH2+HI2,代入求出即可.
+x,根据勾股定理得出OI2=OH2+HI2,代入求出即可.解答:(1)证明:∵IJ∥EF,IH∥ED,
∴
 ,
, ,
,∴
 .
.(2)四边形GHIJ是正方形,
证明:∵CDEF是正方形,
∴EF=DE=CD=CF,
∵
 =
= ,
,∴JI=HI,
∵IH∥ED,IJ∥EF,JG∥FC,
∴IJ∥DH,IH∥JG,∠IHG=∠EDC=90°,
∴四边形GHIJ是正方形.
(3)解:设正方形GHIJ的边长为x,则GH=HI=JG=x,在直角三角形△OGJ,∠GOJ=30°,
∴OG=
 ,OH=
,OH= +x,∵OI2=OH2+HI2,
+x,∵OI2=OH2+HI2,∴
 ,
,解得:
 ,
,∴正方形GHIJ的面积是4.3cm2.
点评:本题考查了正方形的性质和判定,勾股定理,平行线分线段成比例定理等知识点的应用,关键是证出正方形GHIJ和根据含30度的直角三角形的性质得出方程,题目比较典型.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目

 (2011•台州模拟)如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.
(2011•台州模拟)如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.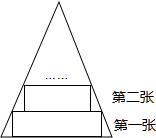 一张等腰三角形纸片,底边长13cm,底边上的高长为32.5cm.现沿底边依次从下往上裁剪宽度均为5cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
一张等腰三角形纸片,底边长13cm,底边上的高长为32.5cm.现沿底边依次从下往上裁剪宽度均为5cm的矩形纸条,如图所示,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( ) 如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.
如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.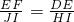 吗?
吗?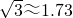 ,结果精确到0.1cm2)?
,结果精确到0.1cm2)?