题目内容
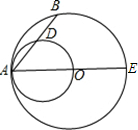已知⊙O的半径为OA=2cm，以OA为直径的⊙C与⊙O的弦AB交于点D，若BD=1cm，则AB=________cm．
2
分析：连接OD，BE，易证得OD∥BE，再根据比例线段，可求出AB的值．
解答：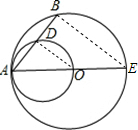
解：如图，连接OD．
∵OA是⊙C的直径，AE是⊙O的直径，
∴∠ADO=∠ABE=90°，
∴OD∥BE，
∴AD：AB=AO：AE=1：2，
∴AB=2AD=2BD=2．
故答案填2．
点评：此题运用了圆内切的有关知识，以及相似三角形的判定和性质、弦切角定理，圆周角定理等，综合性比较强．
分析：连接OD，BE，易证得OD∥BE，再根据比例线段，可求出AB的值．
解答：
解：如图，连接OD．∵OA是⊙C的直径，AE是⊙O的直径，
∴∠ADO=∠ABE=90°，
∴OD∥BE，
∴AD：AB=AO：AE=1：2，
∴AB=2AD=2BD=2．
故答案填2．
点评：此题运用了圆内切的有关知识，以及相似三角形的判定和性质、弦切角定理，圆周角定理等，综合性比较强．
练习册系列答案
相关题目
10、已知⊙O的半径为OA=2cm，以OA为直径的⊙C与⊙O的弦AB交于点D，若BD=1cm，则AB=
