Question

△ABC中，∠A=45°，∠C=120°，BC=2，则AC=________．

Answer 1

分析：首先延长AC，过点B作BE⊥AC于点E，利用直角三角形中30°所对的边等于斜边的一半，求出CE=1，再利用勾股定理求出BE=，近而利用等腰直角三角形的性质求出AE的长，即可得出答案．
解答：解：延长AC，过点B作BE⊥AC于点E，
∵∠C=120°，
∴∠ECB=60°
∵∠BEC=90°，
∴∠EBC=30°，
∵BC=2，
∴CE=1，
∴BE==，
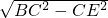∵∠A=45°，∠E=90°，
∴∠EBA=45°，
∴AE=BE=，
∴AC=AE-EC=-1．
故答案为：-1．
点评：此题主要考查了利用直角三角形中30°所对的边等于斜边的一半以及勾股定理等知识，作出Rt△BCE是解题关键．