题目内容

若|x-1|＜
1
1000
，|y-1|＜
1
1000
，求x+y与x-y的取值范围．
分析：首先解绝对值不等式即可求得x，y的值的范围，则x+y与x-y的范围即可求得．
解答：解：∵|x-1|＜
1
1000
，
∴-
1
1000
＜x-1＜
1
1000
，
则
999
1000
＜x＜
1001
1000
，
同理，
999
1000
＜y＜
1001
1000
，
∴
999
1000
+
999
1000
＜x+y＜
1001
1000
+
1001
1000
，即
999
500
＜x+y＜
1001
500
，
999
1000
-
1001
1000
＜x-y＜
1001
1000
-
999
1000
，即-
1
500
＜x-y＜
1
500
．
点评：本题考查了绝对值不等式的解法，正确去掉绝对值符号是关键．
练习册系列答案
相关题目
15、如图，DE∥BC，CF为BC的延长线，若∠ADE=50°，∠ACF=110°，则∠A的度数是（　　）
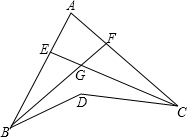精英家教网（1）如图，BE是∠ABD的平分线．CF是∠ACD的平分线，BE与CF交于G，若∠BDC=140°，∠BGC=110°，求∠A的大小．
（2）在△ABC中，∠A=50°，高BE、CF交于O，且O不与B、C重合，求∠BOC的度数．
有两段长度相等的河渠挖掘任务，分别交给甲、乙两个工程队同时进行挖掘，计划1天内完成，图中反映这天上午所挖掘河渠长度y（米）与挖掘时间x（小时）之间的关系．
精英家教网
（1）图中线段OB表示
 
（选填甲队、乙队）的图象；
（2）求出线段CD所对应的函数关系式；
（3）若挖掘任务都是110米，下午甲队挖掘速度不变，问乙队的速度增加多少？才能使两队同时完成任务．
精英家教网如图，BF是∠ABD的平分线，CE是∠ACD的平分线，BE与CE交于G，若∠BDC=140°，∠BGC=110°，则∠A的度数为（　　）
A、50°B、55°C、70°D、80°
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D、C分别在M、N的位置上，若∠EFG=55°则∠2=
110°
110°
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

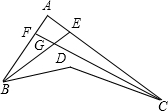精英家教网