题目内容
函数y=(x-1)2+3的最小值为 ,抛物线y=x2-2x+3的顶点坐标是 .
考点:二次函数的最值,二次函数的性质
专题:计算题
分析:根据二次函数的性质易得y=(x-1)2+3的最小值;先把为y=x2-2x+3配成顶点式,然后根据二次函数性质求出顶点坐标.
解答:解:函数y=(x-1)2+3的最小值为3,;
因为y=x2-2x+3=(x-1)2+2,所以抛物线y=x2-2x+3的顶点坐标是(1,2).
故答案为3,(1,2).
因为y=x2-2x+3=(x-1)2+2,所以抛物线y=x2-2x+3的顶点坐标是(1,2).
故答案为3,(1,2).
点评:本题考查了二次函数y=ax2+bx+c的最值:当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=-
时,y=
.当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值,当x=-
时,y=
.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
下列二次根式,属于最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图是某中学景点内的一个拱门,它是⊙O的一部分,已知拱门的地面宽度CD=2m,它的最大高度EM=3m,则构成拱门的⊙O的半径是
如图是某中学景点内的一个拱门,它是⊙O的一部分,已知拱门的地面宽度CD=2m,它的最大高度EM=3m,则构成拱门的⊙O的半径是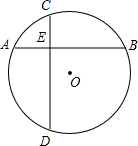 如图,已知在⊙O中,AB,CD两弦互相垂直于点E,AB被分成4cm和10cm两段.
如图,已知在⊙O中,AB,CD两弦互相垂直于点E,AB被分成4cm和10cm两段. 双曲线y1、y2在第一象限的图象如图,过y1=
双曲线y1、y2在第一象限的图象如图,过y1=