题目内容
金陵中学的同学们到灵谷寺开展社会实践活动，他们通过测量计算出灵谷塔的高度．他们在C点测得塔顶A的仰角是点的仰角是45°，向着塔的方向走了28m到达D点后，测得A点的仰角是60°．请你帮他们求出灵谷塔的高度．（| 3 |
分析：设AB=xm，在直角△ABC中，利用三角函数可以利用x表示出BC的长，同理在直角△ABD中利用三角函数表示出BD的长，根据CD+BD=BC即可列方程求得x的值．
解答：解：设AB=xm．
在△ABC中，∠ABC=90°，tanC=tan450=
=1，
∴BC=AB=xm．
在△ABD中，∠ABD=90°，tan∠ADB=tan600=
=
，
∴BD=
AB=
=
xm．
∵CD+BD=BC，∴
x+28=x，
解之，得x=14(3+
)≈66（m）．
答：灵谷塔的高度约是66m．
在△ABC中，∠ABC=90°，tanC=tan450=
| AB |
| BC |
∴BC=AB=xm．
在△ABD中，∠ABD=90°，tan∠ADB=tan600=
| AB |
| BD |
| 3 |
∴BD=
| 3 |
| x | ||
|
| ||
| 3 |
∵CD+BD=BC，∴
| ||
| 3 |
解之，得x=14(3+
| 3 |
答：灵谷塔的高度约是66m．
点评：本题考查仰角的定义以及方程思想，要求学生能借助仰角构造直角三角形并解直角三角形．
练习册系列答案
相关题目
金陵中学的同学们到灵谷寺开展社会实践活动，他们通过测量计算出灵谷塔的高度．他们在C点测得塔顶A的仰角是点的仰角是45°，向着塔的方向走了28m到达D点后，测得A点的仰角是60°．请你帮他们求出灵谷塔的高度．（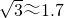
，结果保留整数）
金陵中学的同学们到灵谷寺开展社会实践活动，他们通过测量计算出灵谷塔的高度．他们在C点测得塔顶A的仰角是点的仰角是45°，向着塔的方向走了28m到达D点后，测得A点的仰角是60°．请你帮他们求出灵谷塔的高度．（
，结果保留整数）