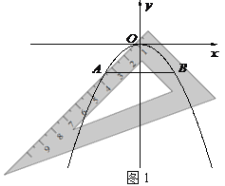
ЬтФПФкШн
ЁОЬтФПЁПСНИіШ§НЧАх![]() ЃЌ
ЃЌ![]() ЃЌАДШчЭМЫљЪОЕФЮЛжУАкЗХЃЌЕу
ЃЌАДШчЭМЫљЪОЕФЮЛжУАкЗХЃЌЕу![]() гыЕу
гыЕу![]() жиКЯЃЌБп
жиКЯЃЌБп![]() гыБп
гыБп![]() дкЭЌвЛЬѕжБЯпЩЯЃЈМйЩшЭМаЮжаЫљгаЕФЕуЃЌЯпЖМдкЭЌвЛЦНУцФкЃЉЃЎЦфжаЃЌ
дкЭЌвЛЬѕжБЯпЩЯЃЈМйЩшЭМаЮжаЫљгаЕФЕуЃЌЯпЖМдкЭЌвЛЦНУцФкЃЉЃЎЦфжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЯжЙЬЖЈШ§НЧАх
ЃЎЯжЙЬЖЈШ§НЧАх![]() ЃЌНЋШ§НЧАх
ЃЌНЋШ§НЧАх![]() биЩфЯп
биЩфЯп![]() ЗНЯђЦНвЦЃЌЕБЕу
ЗНЯђЦНвЦЃЌЕБЕу![]() ТфдкБп
ТфдкБп![]() ЩЯЪБЭЃжЙдЫЖЏЃЎЩшШ§НЧАхЦНвЦЕФОрРыЮЊ
ЩЯЪБЭЃжЙдЫЖЏЃЎЩшШ§НЧАхЦНвЦЕФОрРыЮЊ![]() ЃЌСНИіШ§НЧАхжиЕўВПЗжЕФУцЛ§ЮЊ
ЃЌСНИіШ§НЧАхжиЕўВПЗжЕФУцЛ§ЮЊ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЕБЕу![]() ТфдкБп
ТфдкБп![]() ЩЯЪБЃЌ
ЩЯЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСП
ЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшБп![]() ЕФжаЕуЮЊЕу
ЕФжаЕуЮЊЕу![]() ЃЌБп
ЃЌБп![]() ЕФжаЕуЮЊЕу
ЕФжаЕуЮЊЕу![]() ЃЎжБНгаДГідкШ§НЧАхЦНвЦЙ§ГЬжаЃЌЕу
ЃЎжБНгаДГідкШ§НЧАхЦНвЦЙ§ГЬжаЃЌЕу![]() гыЕу
гыЕу![]() жЎМфОрРыЕФзюаЁжЕЃЎ
жЎМфОрРыЕФзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ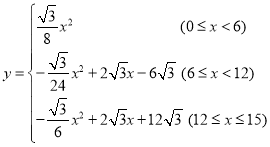 ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃК
ЃЈ1ЃЉгЩШёНЧШ§НЧКЏЪ§ЃЌЕУЕН![]() ЕФГЄЃЌНјЖјПЩЕУ
ЕФГЄЃЌНјЖјПЩЕУ![]() ЕФГЄЃЌгЩОиаЮЕФаджЪЃЌПЩЕУД№АИЃЛ
ЕФГЄЃЌгЩОиаЮЕФаджЪЃЌПЩЕУД№АИЃЛ
ЃЈ2ЃЉЗжРрЬжТлЃКЂйЕБ![]() ЪБЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЃЌПЩЕУД№АИЃЛЂкЕБ
ЪБЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНЃЌПЩЕУД№АИЃЛЂкЕБ![]() ЪБЃЌ
ЪБЃЌ
ЂлЕБ![]() ЪБЃЌИљОнУцЛ§ЕФКЭВюЃЌПЩЕУД№АИЃЛ
ЪБЃЌИљОнУцЛ§ЕФКЭВюЃЌПЩЕУД№АИЃЛ
ЃЈ3ЃЉИљОнЕугыжБЯпЩЯЫљгаЕуЕФСЌЯпжаДЙЯпЖЮзюЖЬЃЌПЩЕУ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌИљОнШ§НЧаЮЕФ
ЩЯЃЌИљОнШ§НЧаЮЕФ
жаЮЛЯпЃЌПЩЕУ![]() ЕФГЄЃЌИљОнШёНЧШ§НЧКЏЪ§ЃЌПЩЕУ
ЕФГЄЃЌИљОнШёНЧШ§НЧКЏЪ§ЃЌПЩЕУ![]() ЕФГЄЃЌИљОнЯпЖЮЕФКЭВюЃЌПЩЕУД№АИЃЎ
ЕФГЄЃЌИљОнЯпЖЮЕФКЭВюЃЌПЩЕУД№АИЃЎ
ЪдЬтНтЮіЃК
НтЃКЃЈ1ЃЉШчЭМ1ЫљЪОЃКзї![]() гк
гк![]() ЕуЃЎ
ЕуЃЎ
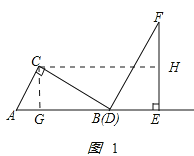
дк![]() жаЃЌгЩ
жаЃЌгЩ![]() ЃЌ
ЃЌ![]() ЃЌЕУЃК
ЃЌЕУЃК![]() =
=![]() ЃЎ
ЃЎ
дк![]() жаЃЌ
жаЃЌ![]() ЃЎЫФБпаЮ
ЃЎЫФБпаЮ![]() ЪЧОиаЮЃЌ
ЪЧОиаЮЃЌ![]() ЃЌЙЪД№АИЮЊЃК
ЃЌЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЕБ![]() ЪБЃЌШчЭМ2ЫљЪОЃЎ
ЪБЃЌШчЭМ2ЫљЪОЃЎ
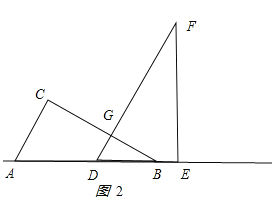
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕУЃК
ЃЌЕУЃК![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
жиЕўВПЗжЕФУцЛ§ЮЊ![]() ЃЛ
ЃЛ
ЂкЕБ![]() ЪБЃЌШчЭМ3ЫљЪОЃЎ
ЪБЃЌШчЭМ3ЫљЪОЃЎ
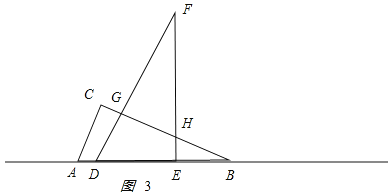
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
жиЕўВПЗжЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
ЛЏМђЃЌЕУ![]() ЃЛ
ЃЛ
ЂлЕБ![]() ЪБЃЌШчЭМ4ЫљЪОЃЎ
ЪБЃЌШчЭМ4ЫљЪОЃЎ
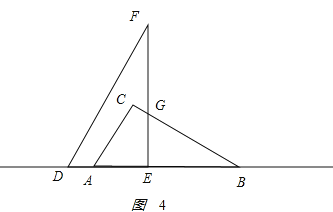
![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
жиЕўВПЗжЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
ЛЏМђЃЌЕУ![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃК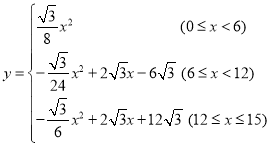 ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ5ЫљЪОзї![]() гк
гк![]() ЕуЃЎ
ЕуЃЎ
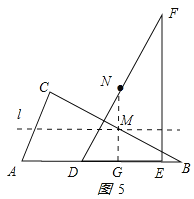
Еу![]() дк
дк![]() ЩЯЪБ
ЩЯЪБ![]() зюЖЬЃЌ
зюЖЬЃЌ![]() ЪЧ
ЪЧ![]() ,
,![]() ЃЎ
ЃЎ ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()