题目内容
18.写出二次函数y=2x2和y=-3x2具有的一个共同性质是对称轴为y轴,顶点坐标为(0,0).分析 利用二次函数的对称轴,顶点坐标,开口方向,最值以及增减性逐一分析得出答案即可.
解答 解:二次函数y=2x2开口向上,对称轴为y轴,顶点坐标为(0,0),当x>0,y随着x的增大而增大,当x<0,y随着x的增大而减小;
y=-3x2开口向下,对称轴为y轴,顶点坐标为(0,0),当x>0,y随着x的增大而减小,当x<0,y随着x的增大而增大;
具有的一个共同性质是:对称轴为y轴,顶点坐标为(0,0).
故答案为:对称轴为y轴,顶点坐标为(0,0).
点评 此题考查二次函数的性质,掌握二次函数y=ax2的性质是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.下面的图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.下列各题去括号所得结果正确的是( )
| A. | -2(a+b)=-2a+b | B. | -2(a+b)=-2a-b | C. | -2(a+b)=-2a-2b | D. | -2(a+b)=-2a+2b |

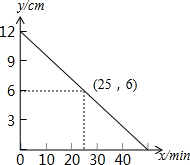 如图,是一根蜡烛的长度y(cm)与燃烧时间x(min)之间函数关系的图象.
如图,是一根蜡烛的长度y(cm)与燃烧时间x(min)之间函数关系的图象.