题目内容
8.计算(1)$\sqrt{27}$-$\sqrt{\frac{1}{3}}$+$\sqrt{12}$
(2)($\sqrt{3}$-1)2-(3+2$\sqrt{2}$)(3-2$\sqrt{2}$)
(3)($\sqrt{54}$-2$\sqrt{15}$)×$\sqrt{3}$-$\frac{2}{3}$$\sqrt{\frac{1}{2}}$.
分析 根据二次根式的性质把二次根式化简,根据二次根式的混合运算法则计算即可.
解答 解:(1)$\sqrt{27}$-$\sqrt{\frac{1}{3}}$+$\sqrt{12}$=3$\sqrt{3}$-$\frac{\sqrt{3}}{3}$+2$\sqrt{3}$=$\frac{14\sqrt{3}}{3}$;
(2)($\sqrt{3}$-1)2-(3+2$\sqrt{2}$)(3-2$\sqrt{2}$)=3-2$\sqrt{3}$+1-9+8=3-2$\sqrt{3}$;
(3)($\sqrt{54}$-2$\sqrt{15}$)×$\sqrt{3}$-$\frac{2}{3}$$\sqrt{\frac{1}{2}}$=$\sqrt{54}$×$\sqrt{3}$-2$\sqrt{15}$×$\sqrt{3}$-$\frac{2}{3}$×$\frac{\sqrt{2}}{2}$=9$\sqrt{2}$-6$\sqrt{5}$-$\frac{\sqrt{2}}{3}$=$\frac{26\sqrt{2}}{3}$-6$\sqrt{5}$.
点评 本题考查的是二次根式的混合运算、掌握二次根式的性质、二次根式的混合运算法则是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
18.“经过有交通信号灯的路口,遇到红灯”这个事件是( )
| A. | 确定性事件 | B. | 随机事件 | C. | 必然事件 | D. | 不可能事件 |
19.下列函数中,满足y的值随x的值增大而增大的是( )
| A. | y=-$\sqrt{2}$x | B. | y=$\frac{4}{x}$ | C. | y=3x-2016 | D. | y=x2 |
 如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,且CD:AD=2:3,AC=10cm,则点D到AB的距离等于4cm.
如图,在△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D,且CD:AD=2:3,AC=10cm,则点D到AB的距离等于4cm. 如图,已知PB⊥AB,PC⊥AC,且PB=PC,D是AP上的一点,求证:BD=CD.
如图,已知PB⊥AB,PC⊥AC,且PB=PC,D是AP上的一点,求证:BD=CD.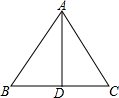 如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程说明△ABD≌△ACD的理由.
如图,已知△ABC中,AB=AC,AD平分∠BAC,请补充完整过程说明△ABD≌△ACD的理由.