题目内容
如图，若P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1、P2，连接P1P2交OA于M，交OB于N，P1P2=24，则△PMN的周长是考点：轴对称的性质
专题：
分析：先根据轴对称的性质得出PM=P1M，PN=P2N，由此可得出结论．
解答：解：∵P点关于OA、OB的对称点为P1、P2，
∴PM=P1M，PN=P2N，
∴△PMN的周长=PM+PN+MN=P1P2=24．
故答案为：24．
∴PM=P1M，PN=P2N，
∴△PMN的周长=PM+PN+MN=P1P2=24．
故答案为：24．
点评：本题考查的是轴对称的性质，熟知如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线是解答此题的关键．
练习册系列答案
相关题目
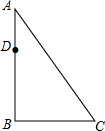如图，AB为一棵大树，在树上距地面10m的D处有两只猴子，它们同时发现地面上的C处有一筐水果，一只猴子从D处上爬到树顶A处，利用拉在A处的滑绳AC，滑到C处，另一只猴子从D处滑到地面B，再由B跑到C，已知两猴子所经路程都是30m，求树高AB．
如图，矩形ABCD中，AB=20cm，BC=4cm，点P从A 开始沿折线A-B-C-D以4cm/s的速度运动，点Q从C开始沿CD边以1cm/s的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达D时，另一点也随之停止运动，设运动时间为t（s），当t=