题目内容
对于正整数a，我们规定：若a为奇数，则f（a）=3a+1；若a为偶数，则
．例如f（15）=3×15+1=46，
．若a1=8，a2=f（a1），a3=f（a2），a4=f（a3），…，依此规律进行下去，得到一列数a1，a2，a3，a4，…，an，…（n为正整数），则a3=________，a1+a2+a3+…+a2014=________．
2 4705
分析：按照规定：若a为奇数，则f（a）=3a+1；若a为偶数，则，直接运算得出a3，进一步找出规律解决问题．
解答：a1=8，a2=
=4，a3=
=2，a4=
=1，a5=1×3+1=4，a6==2，…，
这一列数按照除a1外，按照4、2、1三个数一循环，
∵2013÷3=671，
∴a1+a2+a3+…+a2014=8+（4+2+1）×671=8+4697=4705．
故答案为：2；4705．
点评：此题考查数列的规律，通过运算得出规律，进一步利用规律解决问题．
分析：按照规定：若a为奇数，则f（a）=3a+1；若a为偶数，则
，直接运算得出a3，进一步找出规律解决问题．解答：a1=8，a2=
=4，a3==2，a4==1，a5=1×3+1=4，a6==2，…，这一列数按照除a1外，按照4、2、1三个数一循环，
∵2013÷3=671，
∴a1+a2+a3+…+a2014=8+（4+2+1）×671=8+4697=4705．
故答案为：2；4705．
点评：此题考查数列的规律，通过运算得出规律，进一步利用规律解决问题．
练习册系列答案
相关题目
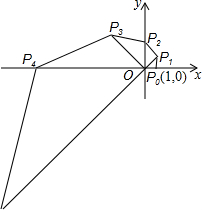如图，在直角坐标系中，已知点P0的坐标为（1，0），将线段OP0按逆时针方向旋转45°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转45°，长度伸长为OP1的2倍，得到线段OP2；如此下去，得到线段OP3，OP4，…，OPn（n为正整数）．我们规定：把点Pn（xn，yn）（n=0，1，2，3，…）的横坐标xn、纵坐标yn都取绝对值后得到的新坐标（|xn|，|yn|）称之为点Pn的“绝对坐标”．则Pn的“绝对坐标”为（ ）A、（2n-1
| ||||
| B、（2n，0）或（0，2n） | ||||
C、（0，2n）或（2n-1
| ||||
D、（2n-1
|
，
）或（2n，0）
，
）
，
）或（2n，0）或（0，2n）
，
）或（2n，0）
，
）
，
）或（2n，0）或（0，2n）
，
）或（2n，0）
，
）
，
）或（2n，0）或（0，2n）