题目内容
(1)已知,如图1,△ABC的周长为l,面积为S,其内切圆圆心为0,半径为r,求证:r=| 2S | l |
(2)已知,如图2,△ABC中,A、B、C三点的坐标分别为A(-3,O)、B(3,0)、C(0,4).若△ABC内心为D.求点D坐标;
(3)与三角形的一边和其他两边的延长线相切的圆,叫旁切圆,圆心叫旁心.请求出条件(2)中的△ABC位于第一象限的旁心的坐标.
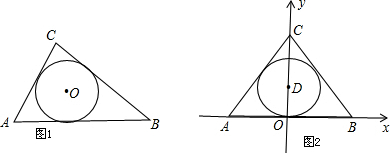
分析:(1)连接0A、OB、OC,设ABC的三边分别为a、b、c,根据:S=S△OAC+S△OBC+S△OAB即可证得;
(2)首先求得内切圆的半径,即可确定D的坐标;
(3)设∠B和∠C的外角平分线交于点P,则点P为旁心,过点P分别为作PE⊥x轴于E,PF⊥CB于F,则PF=PE=OC=4,在Rt△PFC中,利用三角函数即可求解.
(2)首先求得内切圆的半径,即可确定D的坐标;
(3)设∠B和∠C的外角平分线交于点P,则点P为旁心,过点P分别为作PE⊥x轴于E,PF⊥CB于F,则PF=PE=OC=4,在Rt△PFC中,利用三角函数即可求解.
解答: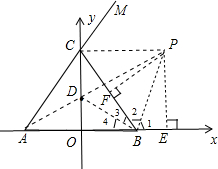 证明:连接0A、OB、OC,设AB、CA,BC的三边分别为a、b、c,
证明:连接0A、OB、OC,设AB、CA,BC的三边分别为a、b、c,
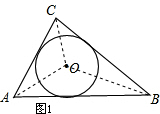
则:S=S△OAC+S△OBC+S△OAB(1分)
=
br+
ar+
cr
=
(a+b+c)r=
lr
∴r=
(3分)
(2)∵A(-3,O),B(3,O),C(0,4)
∴AB=6,AC=BC=5(4分)l=AB+AC+BC=16,S=
AB•OC=12(5分)
由条件(1)得:r=
=
=
,得D(0,
)(6分)
(3)方法一:设∠B和∠C的外角平分线交于点P,则点P为旁心(7分)
∵∠MCB=2∠PCB=2∠CBA
∴∠PCB=∠CBA
∴CP∥AB(8分)
过点P分别为作PE⊥x轴于E,PF⊥CB于F,则PF=PE=OC=4(10分)
在Rt△PFC中,PC=
=
=
=5
∴P(5,4)(12分)
方法二:过点B作∠B的外角平分线交AD的延长线于点P,则点P为旁心,(7分)
过点P作PE⊥x轴于E,连接BD,令P(a,b)
由∠1=∠2,∠3=∠4得:
∠1+∠4=∠2+∠3=90°
∴Rt△DOB∽Rt△BEP,∴
=
化简得:b=2a-6(1)(9分)
由Rt△AOD∽Rt△AEP得:
=
化简得:2b=a+3(2)(11分)
联立(1)、(2)解得a=5,b=4,∴P(5,4)
 证明:连接0A、OB、OC,设AB、CA,BC的三边分别为a、b、c,
证明:连接0A、OB、OC,设AB、CA,BC的三边分别为a、b、c,
则:S=S△OAC+S△OBC+S△OAB(1分)
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
∴r=
| 2S |
| l |
(2)∵A(-3,O),B(3,O),C(0,4)
∴AB=6,AC=BC=5(4分)l=AB+AC+BC=16,S=
| 1 |
| 2 |
由条件(1)得:r=
| 2S |
| l |
| 2×12 |
| 16 |
| 3 |
| 2 |
| 3 |
| 2 |
(3)方法一:设∠B和∠C的外角平分线交于点P,则点P为旁心(7分)
∵∠MCB=2∠PCB=2∠CBA
∴∠PCB=∠CBA
∴CP∥AB(8分)
过点P分别为作PE⊥x轴于E,PF⊥CB于F,则PF=PE=OC=4(10分)
在Rt△PFC中,PC=
| PF |
| sin∠PCF |
| PF |
| sin∠CBO |
| 4 | ||
|
∴P(5,4)(12分)
方法二:过点B作∠B的外角平分线交AD的延长线于点P,则点P为旁心,(7分)
过点P作PE⊥x轴于E,连接BD,令P(a,b)
由∠1=∠2,∠3=∠4得:
∠1+∠4=∠2+∠3=90°
∴Rt△DOB∽Rt△BEP,∴
| b |
| a-3 |
| 3 | ||
|
化简得:b=2a-6(1)(9分)
由Rt△AOD∽Rt△AEP得:
| 3 |
| a+3 |
| ||
| b |
化简得:2b=a+3(2)(11分)
联立(1)、(2)解得a=5,b=4,∴P(5,4)
点评:本题主要考查了三角形的内心与外接圆,解这类题一般都利用过内心向正三角形的一边作垂线,则正三角形的半径、内切圆半径和正三角形边长的一半构成一个直角三角形,解这个直角三角形,可求出相关的边长或角的度数.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为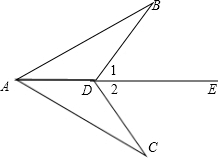 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为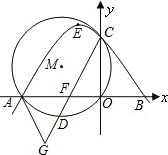 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧