题目内容
【题目】如图所示，A，B两个建筑物分别位于河的两岸，要测得它们之间的距离，可以从B出发沿河岸画一条射线BF，在BF上截取BC＝CD，过D作DE∥AB，使E，C，A在同一条直线卜，则DE的长就等于A，B之间的距离，请你说明道理．
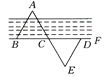
【答案】见解析.
【解析】【试题分析】因为AB∥DE，所以∠A＝∠E或∠ABC＝∠EDC，因为BC＝CD，根据AAS证明ΔABC≌ΔEDC，所以AB＝ED.从而得证.
【试题解析】
由题意并结合图形可以知道BC＝CD，∠ACB＝∠ECD，又AB∥DE，从而∠A＝∠E或∠ABC＝∠EDC，故在ΔABC与ΔEDC中，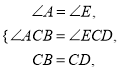 
所以ΔABC≌ΔEDC
(AAS)，所以AB＝ED，即测出ED的长后即可知道A，B之间的距离．
练习册系列答案
相关题目
【题目】如图，从左到右，在每个小格子都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等．
|
|
|
|
|
|
|
（
）可求得
__________．第
个格子中的数为__________．
（
）判断：前
个格子中所填整数之和是否可能为
？若能，求出
的值；若不能，请说明理由．
（
）如果
、
为前三个格子中的任意两个数，那么所有的
的和可以通过计算：
得到，若
， 
为前
个格子中的任意两个数，则所有的
的和为__________．
