题目内容
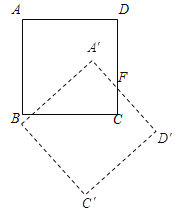
如图所示,正方形ABCD的边长等于2,它绕顶点B按顺时针方向旋转得到正方形A′BC′D′.在这个旋转过程中:
(1)旋转中心是什么?
(2)若旋转角为45°,边CD与A′D′交于F,求DF的长度.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
题目内容
如图所示,正方形ABCD的边长等于2,它绕顶点B按顺时针方向旋转得到正方形A′BC′D′.在这个旋转过程中:
(1)旋转中心是什么?
(2)若旋转角为45°,边CD与A′D′交于F,求DF的长度.


 寒假学与练系列答案
寒假学与练系列答案