��Ŀ����
 ͨ��ѧϰ���Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת�������Ƶģ������ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ����������ԣ�sad������ͼ�٣��ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsadA=�ױ�/��=
ͨ��ѧϰ���Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת�������Ƶģ������ڵ����������н����߽�֮�����ϵ�����Ƕ��壺�����������еױ������ıȽ����������ԣ�sad������ͼ�٣��ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsadA=�ױ�/��=| BC |
| AB |
��1��sad60��=
��2������0�㣼A��180�㣬��A������ֵsadA��ȡֵ��Χ��
��3����ͼ�ڣ���֪sinA=
| 3 |
| 5 |
��������1�����ݵ��������ε����ʣ�����ǵĶ������жϳ�������Ϊ�ȱ������Σ��ٸ������ԵĶ�����
��2�����0�Ⱥ�180��ʱ���������ε����ıȼ��ɣ�
��3������ֱ�ǡ�ABC���������������ACD���������ԵĶ�����
��2�����0�Ⱥ�180��ʱ���������ε����ıȼ��ɣ�
��3������ֱ�ǡ�ABC���������������ACD���������ԵĶ�����
����⣺��1���������Զ��壬
������Ϊ60��ʱ�����������ε�Ϊ60�㣬
��������Ϊ�ȱ������Σ�
��sad60��=
=1��
�ʴ�Ϊ��1��
��2������A�ӽ�0��ʱ��sadA�ӽ�0��
����A�ӽ�180��ʱ�����������εĵӽ������Ķ�������sadA�ӽ�2��
����sadA��ȡֵ��Χ��0��sadA��2��
�ʴ�Ϊ0��sadA��2��
��3����ͼ���ڡ�ABC�У���ACB=90�㣬sin��A=
��
��AB��ȡ��D��ʹAD=AC������CD����DH��AC��HΪ���㣬��BC=3k��AB=5k��
��AD=AC=
=4k��
���ڡ�ADH�У���AHD=90�㣬sinA=
��
��DH=ADsinA=
k��AH=
=
k��
���ڡ�CDH�У�CH=AC-AH=
k��CD=
=
k��
�����ڡ�ACD�У�AD=AC=4k��CD=
k��
�����ԵĶ���ɵã�sadA=
=
��
������Ϊ60��ʱ�����������ε�Ϊ60�㣬
��������Ϊ�ȱ������Σ�
��sad60��=
| 1 |
| 1 |
�ʴ�Ϊ��1��
��2������A�ӽ�0��ʱ��sadA�ӽ�0��
����A�ӽ�180��ʱ�����������εĵӽ������Ķ�������sadA�ӽ�2��
����sadA��ȡֵ��Χ��0��sadA��2��
�ʴ�Ϊ0��sadA��2��
��3����ͼ���ڡ�ABC�У���ACB=90�㣬sin��A=
| 3 |
| 5 |

��AB��ȡ��D��ʹAD=AC������CD����DH��AC��HΪ���㣬��BC=3k��AB=5k��
��AD=AC=
| (5k)2-(3k)2 |
���ڡ�ADH�У���AHD=90�㣬sinA=
| 3 |
| 5 |
��DH=ADsinA=
| 12 |
| 5 |
| AD2-DH2 |
| 16 |
| 5 |
���ڡ�CDH�У�CH=AC-AH=
| 4 |
| 5 |
| DH2+CH2 |
4
| ||
| 5 |
�����ڡ�ACD�У�AD=AC=4k��CD=
4
| ||
| 5 |
�����ԵĶ���ɵã�sadA=
| CD |
| AD |
| ||
| 5 |
������������һ���¶������Ŀ��������������һ�����ݣ�Ҫ��Ϥ���Ǻ����Ķ��壬�ɽ�����Ƚ��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ͨ��ѧϰ���Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת�������Ƶģ������ڵ����������н����߽�֮�����ϵ�����壺�����������еױ������ıȽ������ǵ����ԣ�sad������ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsadA=
ͨ��ѧϰ���Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת�������Ƶģ������ڵ����������н����߽�֮�����ϵ�����壺�����������еױ������ıȽ������ǵ����ԣ�sad������ͼ���ڡ�ABC�У�AB=AC������A�����Լ���sadA����ʱsadA= ������֪��һ���ǵĴ�С��������ǵ�����ֵҲ���Ψһȷ���ġ����������ǵ����Զ��壬���������⣺
������֪��һ���ǵĴ�С��������ǵ�����ֵҲ���Ψһȷ���ġ����������ǵ����Զ��壬���������⣺
 ������sadD��ֵ��
������sadD��ֵ�� ������֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ���ģ����������ǵ����Զ��壬���������⣺
������֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ���ģ����������ǵ����Զ��壬���������⣺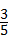 �����С�AΪ��ǣ�����sadA��ֵ��
�����С�AΪ��ǣ�����sadA��ֵ��
 ������֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ���ģ����������ǵ����Զ��壬���������⣺
������֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ���ģ����������ǵ����Զ��壬���������⣺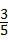 �����С�AΪ��ǣ�����sadA��ֵ��
�����С�AΪ��ǣ�����sadA��ֵ��